题目内容
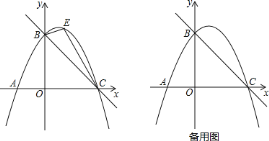
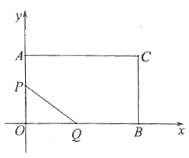
【题目】（问题原型）在图①的矩形
中，点
、
、
、
分别在
、
、
、
上，若
，则称四边形
为矩形的反射四边形；
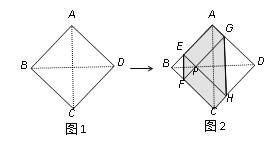
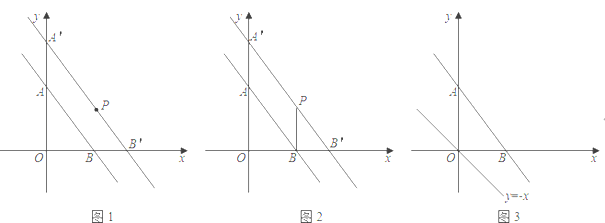
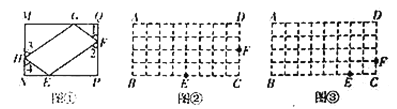
（操作与探索）在图②，图③的矩形
中，
，
，点、分别在
、
边的格点上，试利用正方形网格分别在图②、图③上作矩形的反射四边形；
（发现与应用）由前面的操作可以发现，一个矩形有不同的反射四边形，且这些反射四边形的周长都相等.若在图①的矩形中，
，
，则其反射四边形的周长为______.
【答案】操作与探索:见解析：发现与应用：10.
【解析】
（1）根据网格作出相等的角即可得到反射四边形；
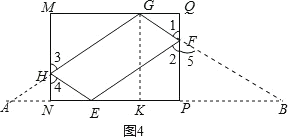
（2）延长GH交PN的延长线与点A，证明△FPE≌△FPB，根据全等三角形的性质得到AB=2NP,再证明GA=GB,过点G作GK⊥NP于K，根据等腰三角形的性质求出KB=
AB=4，再利用勾股定理求出GB的长，即可求出四边形EFGH的周长.
（1）作图如下：
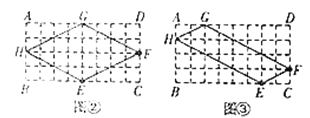
（2）延长GH交PN的延长线与点A，过点G作GK⊥NP于K，
∵∠1=∠2，∠1=∠5，∴∠2=∠5，
又PF=PF,∠FPE=∠FPB，
∴△FPE≌△FPB，
∴EF=BF,EP=PB,
同理AH=EH,NA=EN,
∴AB=2NP=8，
∵∠B=90°-∠5=90°-∠1，∠A=90°-∠3，
∴∠A=∠B，∴GA=GB,
则KB=AB=4，∴GB=
∴四边形EFGH的周长为2GB=10.
练习册系列答案
相关题目
