题目内容
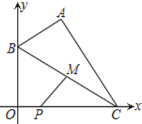
【题目】在平面直角坐标系中，已知
、
，B为y轴上的动点，以AB为边构造
，使点C在x轴上，
为BC的中点，则PM的最小值为______．
【答案】
【解析】
如图，作AH⊥y轴于H，CE⊥AH于E．则四边形CEHO是矩形，OH=CE=4，由△AHB∽△CEA，得
，推出
，推出AE=2BH，设BH=x则AE=2x，推出B（0，4﹣x），C（2+2x，0），由BM=CM，推出M（1+x，
），可得PM
，由此即可解决问题．
如图，作AH⊥y轴于H，CE⊥AH于E．则四边形CEHO是矩形，OH=CE=4．
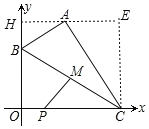
∵∠BAC=∠AHB=∠AEC=90°，∴∠ABH+∠HAB=90°，∠HAB+∠EAC=90°，∴∠ABH=∠EAC，∴△AHB∽△CEA，∴，∴，∴AE=2BH，设BH=x则AE=2x，∴OC=HE=2+2x，OB=4﹣x，∴B（0，4﹣x），C（2+2x，0）．
∵BM=CM，∴M（1+x，）．
∵P（1，0），∴PM，∴x
时，PM有最小值，最小值为．
故答案为：．
练习册系列答案
相关题目
