题目内容
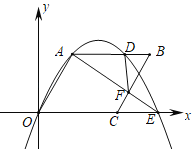
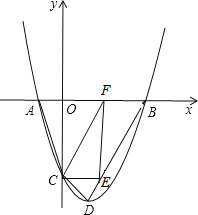
【题目】如图抛物线y=x2+bx+c(c<0)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C,顶点为D,且OB=OC=3,点E为线段BD上的一个动点,EF⊥x轴于F.
(1)求抛物线的解析式;
(2)是否存在点E,使△ECF为直角三角形?若存在,求点E的坐标;不存在,请说明理由;
(3)连接AC、BC,若点P是抛物线上的一个动点,当P运动到什么位置时,∠PCB=∠ACO,请直接写出点P的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)存在,(![]() ,﹣3)或(3
,﹣3)或(3![]() ﹣3,6
﹣3,6![]() ﹣12);(3)(
﹣12);(3)(![]() ,﹣
,﹣![]() )或(4,5)
)或(4,5)
【解析】
(1)易求得点B,C坐标,即可求得b、c的值,即可解题;
(2)易求得顶点D的坐标,即可求得直线BD的解析式,根据∠CEF=90°,即可求得点E纵坐标为﹣3,即可解题;
(3)存在2种情况:①∠PCB=∠ACO,②∠P'CB=∠ACO,可分别求得tan∠PCE的值,即可求得直线PC斜率,即可求得直线PC于抛物线交点P坐标,即可解题.
解:(1)∵OB=OC=3,
∴点B坐标为(3,0),点C坐标为(0,﹣3),
∵抛物线y=x2+bx+c经过点B,C,∴![]() ,
,
解得:c=﹣3,b=﹣2,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)∵抛物线的解析式为y=x2﹣2x﹣3,
∴点D坐标为(1,﹣4),
∵直线BD经过点B,D,设直线BD解析式为y=kx+b,
则![]() ,
,
解得:k=2,b=﹣6,
∴直线BD解析式为y=2x﹣6,
∵△ECF为直角三角形,
当∠CEF=90°时,E点纵坐标和等于C点纵坐标,
∴点E纵坐标为﹣3,
∴点E横坐标为![]() ,
,
∴点E坐标为(![]() ,﹣3);
,﹣3);
当∠FCE=90°时,
∵EF⊥x轴,所以易得△CFO∽FEC,
∴![]() ,即EFOC=CF2,=OF2+OC2,
,即EFOC=CF2,=OF2+OC2,
设OF=m,因此F的坐标为(m,0)代入直线BD的方程y=2x﹣6得E的坐标为(m,2m﹣6),
∴EF=6﹣2m,
∴(6﹣2m)×3=m2+9,解得m=3![]() ﹣3(负值舍去),
﹣3(负值舍去),
∴点E的坐标为(3![]() ﹣3,6
﹣3,6![]() ﹣12)
﹣12)
综上可得存在这样的点E,E点的坐标为(![]() ,﹣3)或(3
,﹣3)或(3![]() ﹣3,6
﹣3,6![]() ﹣12).
﹣12).
(3)存在2种情况:
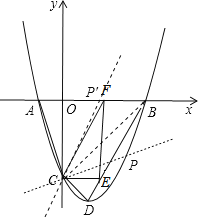
①∠PCB=∠ACO,
∵∠BCE=45°,
∴tan∠BCE=1,
∵tan∠ACO=![]() ,
,
∴tan∠PCB=![]() ,
,
∴tan∠PCE=tan(∠BCE﹣∠PCB)=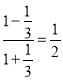 ,
,
∵直线PC经过点P,
∴直线PC解析式为:y=![]() x﹣3,
x﹣3,
∴点P坐标为:(![]() ,﹣
,﹣![]() ),
),
②∠P'CB=∠ACO,
∵∠BCE=45°,
∴tan∠BCE=1,
∵tan∠ACO=![]() ,
,
∴tan∠P'CB=![]() ,
,
∴tan∠P'CE=tan(∠BCE﹣∠P'CB)=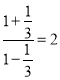 ,
,
∵直线PC经过点P,
∴直线PC解析式为:y=2x﹣3,
∴点P坐标为:(4,5).

 导学教程高中新课标系列答案
导学教程高中新课标系列答案