Question

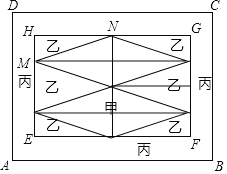
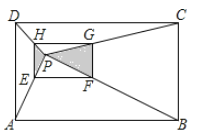
【题目】如图，P是矩形ABCD内一点，连结P与矩形ABCD各顶点，矩形EFGH各顶点分别在边AP，BP，CP，DP上，已知AE＝2EP，EF∥AB，图中两块阴影部分的面积和为S．则矩形ABCD的面积为（　　）

A.4SB.6SC.12SD.18S

Answer 1

【答案】D

【解析】

先证明△PEH∽△PAD，并求相似比为1:3，由此可得（）2，同理可求得，再根据S△PAD+S△PBCS矩形ABCD和S△PEH+S△PFG=S,可得结论.

∵AE＝2EP，

∴，

∵四边形ABCD与四边形EFGH是矩形，

∴∠DAB＝∠HEF＝90°，

∵EF∥AB，

∴∠PEF＝∠PAB，

∴∠PEH＝∠PAD，

∴EH∥AD，

同理，FG∥BC，

∵EH∥AD，

∴△PEH∽△PAD，且相似比为.

∴（）2，

同理，，

∵S△PAD+S△PBCS矩形ABCD，

∴S（S△PAD+S△PBC）S矩形ABCD，

∴矩形ABCD的面积＝18S．

故选：D．