题目内容
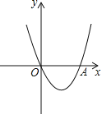
【题目】如图，已知抛物线的顶点在第四象限，顶点到x轴的距离为3，抛物线与x轴交于原点O（0，0）及点A，且OA=4． （1）求该抛物线的解析式； （2）若线段OA绕点O顺时针旋转45°到OA′，试判断点A′是否在该抛物线上，并说明理由．
【答案】（1）
（2）点A′不在该抛物线上，理由见解析.
【解析】
（1）首先求出抛物线的顶点坐标，设抛物线的解析式为y=a（x-2）2+3，由于抛物线经过原点，进而求出a的值即可；
（2）设点A′坐标为（x，y），先求出直线OA′的解析式，根据OA′=OA=4，求出点A′的坐标，进而判断点A′是否在该抛物线上．
解：（1）根据题意可知：抛物线的顶点坐标为（2，-3），
设抛物线的解析式为y=a（x-2）2-3，
由于抛物线经过原点，
即4a-3=0，
解得a=
．
故抛物线的解析式为y=（x-2）2-3；
（2）设点A′坐标为（x，y），
则直线OA′的解析式为y=-x①，
根据旋转的性质可知：OA′=OA=4，
即x2+y2=16②，
由①②可得x=2
，y=-2，
即点A′坐标为（2，-2），
把点A′坐标为（2，-2）代入解析式y=（x-2）2-3；
-2≠（2-2）2-3，
即点A′不在该抛物线上．
练习册系列答案
天天向上口算本系列答案
相关题目
