题目内容
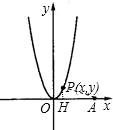
 如图,P是抛物线y=2x2上第一象限内的点,A点坐标为(6,0).
如图,P是抛物线y=2x2上第一象限内的点,A点坐标为(6,0).(1)若P的坐标为(x,y),求△POA的面积S=
(2)指出S是x的什么函数;
(3)当S=6时,求P点的坐标;
(4)在抛物线y=2x2上求出一点P′,使P′O=P′A.答:P′的坐标为
分析:(1)已知A点坐标为(6,0)可以得到OA=6,△POA中OA边上的高就是P点的纵坐标.根据三角形的面积公式就可以求出.
(2)把y=2x2代入(1)中所求的函数解析式,就可以得到S与x之间的函数解析式.判断函数的类型.
(3)把S=6代入(2)中求得的函数解析式,求出x的值,就可以得到P点的坐标.
(4)使P′O=P′A,则P′一定在线段OA的垂直平分线上,OA的垂直平分线的解析式是x=3,因而把x=3代入函数y=2x2的解析式,就可以求出点的纵坐标.
(2)把y=2x2代入(1)中所求的函数解析式,就可以得到S与x之间的函数解析式.判断函数的类型.
(3)把S=6代入(2)中求得的函数解析式,求出x的值,就可以得到P点的坐标.
(4)使P′O=P′A,则P′一定在线段OA的垂直平分线上,OA的垂直平分线的解析式是x=3,因而把x=3代入函数y=2x2的解析式,就可以求出点的纵坐标.
解答:解:(1)过P作PH⊥x轴于H,则S=
OA•PH=
×6•y=3y
(2)∵y=2x2,
∴S=3y=6x2,S是x的二次函数.
(3)当S=6时,3y=6,y=2,6x2=6,
∴x=±1,且P在第一象限,
∴P(1,2).
(4)∵P′O=P′A,则P′在线段OA的中垂线上,
∴P′的横坐标为3,
又当x=3时,y=18,
∴P′(3,18).
| 1 |
| 2 |
| 1 |
| 2 |

(2)∵y=2x2,
∴S=3y=6x2,S是x的二次函数.
(3)当S=6时,3y=6,y=2,6x2=6,
∴x=±1,且P在第一象限,
∴P(1,2).
(4)∵P′O=P′A,则P′在线段OA的中垂线上,
∴P′的横坐标为3,
又当x=3时,y=18,
∴P′(3,18).
点评:本题是二次函数的解析式的求解,与线段的垂直平分线的判定方法,相结合的问题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,P是抛物线C:y=2x2-8x+8对称轴上的一个动点,直线x=k平行于y轴,分别与直线y=x、抛物线C交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,则满足条件的k为
如图,P是抛物线C:y=2x2-8x+8对称轴上的一个动点,直线x=k平行于y轴,分别与直线y=x、抛物线C交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,则满足条件的k为 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 如图,N是抛物线y=x2-2x-3的顶点,且与x轴交于Q、M两点.
如图,N是抛物线y=x2-2x-3的顶点,且与x轴交于Q、M两点. 如图,P是抛物线
如图,P是抛物线