ΧβΡΩΡΎ»ί
 »γΙϊ“ΜΧθ≈ΉΈοœΏy=ax2+bx+cΘ®aΓΌ0Θ©”κx÷α”–ΝΫΗωΫΜΒψΘ§Ρ«Ο¥“‘ΗΟ≈ΉΈοœΏΒΡΕΞΒψΚΆ’βΝΫΗωΫΜΒψΈΣΕΞΒψΒΡ»ΐΫ«–Έ≥ΤΈΣ’βΧθ≈ΉΈοœΏΒΡΓΑ≈ΉΈοœΏ»ΐΫ«–ΈΓ±Θ°
»γΙϊ“ΜΧθ≈ΉΈοœΏy=ax2+bx+cΘ®aΓΌ0Θ©”κx÷α”–ΝΫΗωΫΜΒψΘ§Ρ«Ο¥“‘ΗΟ≈ΉΈοœΏΒΡΕΞΒψΚΆ’βΝΫΗωΫΜΒψΈΣΕΞΒψΒΡ»ΐΫ«–Έ≥ΤΈΣ’βΧθ≈ΉΈοœΏΒΡΓΑ≈ΉΈοœΏ»ΐΫ«–ΈΓ±Θ°Θ®1Θ©ΓΑ≈ΉΈοœΏ»ΐΫ«–ΈΓ±“ΜΕ® «
Β»―ϋ
Β»―ϋ
»ΐΫ«–ΈΘΜΘ®2Θ©»τ≈ΉΈοœΏ≈ΉΈοœΏmΘΚy=aΘ®x-2Θ©2+bΘ®abΘΦ0Θ©ΒΡΓΑ≈ΉΈοœΏ»ΐΫ«–ΈΓ± «÷±Ϋ«»ΐΫ«–ΈΘ§«κ«σ≥ωaΘ§b¬ζΉψΒΡΙΊœΒ ΫΘΜ
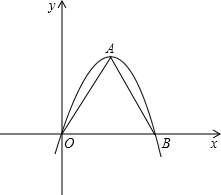
Θ®3Θ©»γΆΦΘ§ΓςOAB «≈ΉΈοœΏnΘΚy=-x2+bΓδxΘ®bΓδΘΨ0Θ©ΒΡΓΑ≈ΉΈοœΏ»ΐΫ«–ΈΓ±Θ§ «Ζώ¥φ‘Ύ“‘‘≠ΒψOΈΣΕ‘≥Τ÷––ΡΒΡΨΊ–ΈABCDΘΩ»τ¥φ‘ΎΘ§«σ≥ωΙΐOΓΔCΓΔD»ΐΒψΒΡ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
Ζ÷ΈωΘΚΘ®1Θ©ΗυΨί≈ΉΈοœΏΒΡΕ‘≥Τ–‘Ϋχ––≈–ΕœΘΜ
Θ®2Θ©”…”Ύ≈ΉΈοœΏ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ§‘ρΒΟΒΫ±ΨΧβ÷–ΒΡΓΑΈοœΏ»ΐΫ«–ΈΓ± «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘Ό»ΖΕ®≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΈΣΘ®2Θ§bΘ©Θ§≈ΉΈοœΏ”κx÷αΝΫΫΜΒψ÷°ΦδΒΡœΏΕΈ≥Λ=2
Θ§»γΚΈΗυΨίΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫ|b|=
ΓΝ2
Θ§»ΜΚσΜ·ΦρΦ¥Ω…ΒΟΒΫa”κbΒΡΙΊœΒΘΜ
Θ®3Θ©ΉςAHΓΆOB”ΎHΒψΘ§œ»ΒΟΒΫBΒψΉχ±ξΈΣΘ®bΓδΘ§0Θ©Θ§AΒψΉχ±ξΈΣΘ®
Θ§
Θ©Θ§‘ΌΗυΨίΨΊ–ΈΒΡ–‘÷ Ω…≈–ΓςOABΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ ΒΟAH=
OBȧ֥
=
bΓδΘ§ΫβΒΟbΓδ=2
Θ§‘ρΩ…»ΖΕ®AΓΔBΝΫΒψΉχ±ξΘ§»ΜΚσΗυΨίΙΊ”Ύ‘≠Βψ÷––ΡΒΡ–‘÷ Ω…»ΖΕ®CΒψ”κDΒψΉχ±ξΘ§ΉνΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≈ΉΈοœΏΒΡΫβΈω ΫΘ°
Θ®2Θ©”…”Ύ≈ΉΈοœΏ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ§‘ρΒΟΒΫ±ΨΧβ÷–ΒΡΓΑΈοœΏ»ΐΫ«–ΈΓ± «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘Ό»ΖΕ®≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΈΣΘ®2Θ§bΘ©Θ§≈ΉΈοœΏ”κx÷αΝΫΫΜΒψ÷°ΦδΒΡœΏΕΈ≥Λ=2
-
|
| 1 |
| 2 |
-
|
Θ®3Θ©ΉςAHΓΆOB”ΎHΒψΘ§œ»ΒΟΒΫBΒψΉχ±ξΈΣΘ®bΓδΘ§0Θ©Θ§AΒψΉχ±ξΈΣΘ®
| bΓδ |
| 2 |
| bΓδ2 |
| 4 |
| ||
| 2 |
| bΓδ2 |
| 4 |
| ||
| 2 |
| 3 |
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©ΓΏ≈ΉΈοœΏ”κx÷α”–ΝΫΗωΫΜΒψΙΊ”Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΕ‘≥ΤΘ§
ΓύΓΑ≈ΉΈοœΏ»ΐΫ«–ΈΓ± «Β»―ϋ»ΐΫ«–ΈΘΜ
Ι ¥πΑΗΈΣΒ»―ϋΘΜ
Θ®2Θ©ΓΏy=aΘ®x-2Θ©2+bΘ®abΘΦ0Θ©ΒΡΓΑ≈ΉΈοœΏ»ΐΫ«–ΈΓ± «÷±Ϋ«»ΐΫ«–ΈΘ§
Γύ¥ΥΓΑΈοœΏ»ΐΫ«–ΈΓ± «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΈΣΘ®2Θ§bΘ©Θ§
Α―y=0¥ζ»κy=aΘ®x-2Θ©2+bΒΟaΘ®x-2Θ©2+b=0Θ§ΫβΒΟx=2Γά
Θ§
Γύ≈ΉΈοœΏy=aΘ®x-2Θ©2+bΘ®abΘΦ0Θ©”κx÷αΝΫΫΜΒψΒΡΉχ±ξΈΣΘ®2+
Θ§0Θ©Θ§Θ®2-
Θ§0Θ©Θ§
Γύ≈ΉΈοœΏy=aΘ®x-2Θ©2+bΘ®abΘΦ0Θ©”κx÷αΝΫΫΜΒψ÷°ΦδΒΡœΏΕΈ≥Λ=2
Θ§
Γύ|b|=
ΓΝ2
Θ§
Γύb2=-
Θ§
Γύab=-1ΘΜ
Θ®3Θ©¥φ‘ΎΘ°ΉςAHΓΆOB”ΎHΒψΘ§»γΆΦΘ§
Α―y=0¥ζ»κy=-x2+bΓδxΒΟ-x2+bΓδx=0Θ§ΫβΒΟx1=0Θ§x2=bΓδΘ§
ΓύBΒψΉχ±ξΈΣΘ®bΓδΘ§0Θ©Θ§
ΓΏy=-x2+bΓδx=-Θ®x-
Θ©2+
Θ§
ΓύAΒψΉχ±ξΈΣΘ®
Θ§
Θ©Θ§
ΓΏΨΊ–ΈABCD“‘‘≠ΒψOΈΣΕ‘≥Τ÷––ΡΘ§
ΓύOA=OB=OC=ODΘ§
ΓύΓςOABΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύAH=
OBȧ
Γύ
=
bΓδΘ§ΫβΒΟbΓδ=2
Θ§
ΓύAΒψΉχ±ξΈΣΘ®
Θ§3Θ©Θ§BΒψΉχ±ξΈΣΘ®2
Θ§0Θ©
ΓύCΒψΉχ±ξΈΣΘ®-
Θ§-3Θ©Θ§DΒψΉχ±ξΈΣΘ®-2
Θ§0Θ©Θ§
…ηΙΐOΓΔCΓΔD»ΐΒψΒΡ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=axΘ®x+2
Θ©Θ§
Α―CΘ®-
Θ§-3Θ©¥ζ»κΒΟa•Θ®-
Θ©Θ®-
+2
Θ©=-3Θ§
ΫβΒΟa=1Θ§
ΓύΥυ«σ≈ΉΈοœΏΒΡ±μ¥ο ΫΈΣy=xΘ®x+2
Θ©=x2+2
xΘ°
ΓύΓΑ≈ΉΈοœΏ»ΐΫ«–ΈΓ± «Β»―ϋ»ΐΫ«–ΈΘΜ
Ι ¥πΑΗΈΣΒ»―ϋΘΜ
Θ®2Θ©ΓΏy=aΘ®x-2Θ©2+bΘ®abΘΦ0Θ©ΒΡΓΑ≈ΉΈοœΏ»ΐΫ«–ΈΓ± «÷±Ϋ«»ΐΫ«–ΈΘ§
Γύ¥ΥΓΑΈοœΏ»ΐΫ«–ΈΓ± «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΈΣΘ®2Θ§bΘ©Θ§
Α―y=0¥ζ»κy=aΘ®x-2Θ©2+bΒΟaΘ®x-2Θ©2+b=0Θ§ΫβΒΟx=2Γά
-
|
Γύ≈ΉΈοœΏy=aΘ®x-2Θ©2+bΘ®abΘΦ0Θ©”κx÷αΝΫΫΜΒψΒΡΉχ±ξΈΣΘ®2+
-
|
-
|
Γύ≈ΉΈοœΏy=aΘ®x-2Θ©2+bΘ®abΘΦ0Θ©”κx÷αΝΫΫΜΒψ÷°ΦδΒΡœΏΕΈ≥Λ=2
-
|
Γύ|b|=
| 1 |
| 2 |
-
|
Γύb2=-
| b |
| a |

Γύab=-1ΘΜ
Θ®3Θ©¥φ‘ΎΘ°ΉςAHΓΆOB”ΎHΒψΘ§»γΆΦΘ§
Α―y=0¥ζ»κy=-x2+bΓδxΒΟ-x2+bΓδx=0Θ§ΫβΒΟx1=0Θ§x2=bΓδΘ§
ΓύBΒψΉχ±ξΈΣΘ®bΓδΘ§0Θ©Θ§
ΓΏy=-x2+bΓδx=-Θ®x-
| bΓδ |
| 2 |
| bΓδ2 |
| 4 |
ΓύAΒψΉχ±ξΈΣΘ®
| bΓδ |
| 2 |
| bΓδ2 |
| 4 |
ΓΏΨΊ–ΈABCD“‘‘≠ΒψOΈΣΕ‘≥Τ÷––ΡΘ§
ΓύOA=OB=OC=ODΘ§
ΓύΓςOABΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύAH=
| ||
| 2 |
Γύ
| bΓδ2 |
| 4 |
| ||
| 2 |
| 3 |
ΓύAΒψΉχ±ξΈΣΘ®
| 3 |
| 3 |
ΓύCΒψΉχ±ξΈΣΘ®-
| 3 |
| 3 |
…ηΙΐOΓΔCΓΔD»ΐΒψΒΡ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=axΘ®x+2
| 3 |
Α―CΘ®-
| 3 |
| 3 |
| 3 |
| 3 |
ΫβΒΟa=1Θ§
ΓύΥυ«σ≈ΉΈοœΏΒΡ±μ¥ο ΫΈΣy=xΘ®x+2
| 3 |
| 3 |
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΝΥ≈ΉΈοœΏΒΡΉέΚœΧβΘΚ λΝΖ’ΤΈ’Εΰ¥ΈΚ· ΐΒΡ–‘÷ Θ§≤Δ«“ΗυΨίΕΰ¥ΈΚ· ΐΒΡ–‘÷ »ΖΕ®ΦΗΚΈΆΦ–ΈΒΡ–‘÷ ΚΆ»ΖΕ®ΒψΒΡΉχ±ξΘΜΜα‘Υ”ΟΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΓΔΒ»±Ώ»ΐΫ«–ΈΚΆΨΊ–ΈΒΡ–‘÷ Ϋ®ΝΔΒ»ΝΩΙΊœΒΘ§ΫΪΚ· ΐΈ ΧβΉΣΜ·ΈΣΖΫ≥ΧΈ ΧβΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ÷ή÷ή«εΦλ≤βœΒΝ–¥πΑΗ
÷ή÷ή«εΦλ≤βœΒΝ–¥πΑΗ «α«…ΕαΙΎ÷ή≤⑬ΩΦ÷±Ά®ΗΏΩΦœΒΝ–¥πΑΗ
«α«…ΕαΙΎ÷ή≤⑬ΩΦ÷±Ά®ΗΏΩΦœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ