题目内容
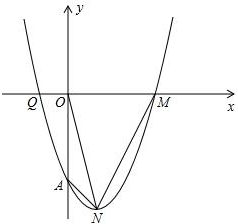 如图,N是抛物线y=x2-2x-3的顶点,且与x轴交于Q、M两点.
如图,N是抛物线y=x2-2x-3的顶点,且与x轴交于Q、M两点.(1)求N点的坐标;
(2)设抛物线顶点为N,与y轴交点为A,求tan∠AON的值;
(3)求四边形OANM的面积.
分析:(1)将抛物线的解析式进行配方,即可得顶点N的坐标.
(2)过N作y轴的垂线,设垂足为B,在Rt△OBN中,由N点的坐标可知OB、BN的长,则∠AON的正切值可求.
(3)四边形OANM的形状不规则,其面积可由图形间的面积和差关系来解,观察图形,可由梯形OBNM的面积减去Rt△ABN的面积求得.
(2)过N作y轴的垂线,设垂足为B,在Rt△OBN中,由N点的坐标可知OB、BN的长,则∠AON的正切值可求.
(3)四边形OANM的形状不规则,其面积可由图形间的面积和差关系来解,观察图形,可由梯形OBNM的面积减去Rt△ABN的面积求得.
解答: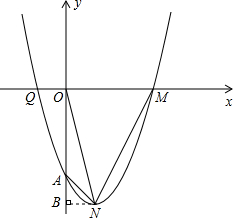 解:(1)∵抛物线y=x2-2x-3=(x-1)2-4,
解:(1)∵抛物线y=x2-2x-3=(x-1)2-4,
∴顶点N(1,-4).
(2)过N作NB⊥y轴于B;
在Rt△OBN中,BN=1,OB=4,则:
tan∠AON=
=
.
(3)由抛物线y=x2-2x-3知,A(0,-3)、M(3,0),即:OA=3,OM=3;
∴S四边形OANM=S梯形OBNM-S△ABN
=
(OM+BN)×OB-
AB×BN
=
×(3+1)×4-
×1×1=7.5
即四边形OANM的面积为7.5.
 解:(1)∵抛物线y=x2-2x-3=(x-1)2-4,
解:(1)∵抛物线y=x2-2x-3=(x-1)2-4,∴顶点N(1,-4).
(2)过N作NB⊥y轴于B;
在Rt△OBN中,BN=1,OB=4,则:
tan∠AON=
| BN |
| OB |
| 1 |
| 4 |
(3)由抛物线y=x2-2x-3知,A(0,-3)、M(3,0),即:OA=3,OM=3;
∴S四边形OANM=S梯形OBNM-S△ABN
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
即四边形OANM的面积为7.5.
点评:此题是二次函数的基础题目,涉及了解直角三角形以及图形面积的解法,作对辅助线即可正确解题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
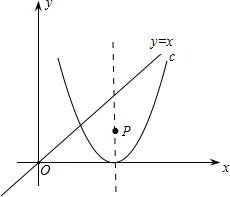 如图,P是抛物线C:y=2x2-8x+8对称轴上的一个动点,直线x=k平行于y轴,分别与直线y=x、抛物线C交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,则满足条件的k为
如图,P是抛物线C:y=2x2-8x+8对称轴上的一个动点,直线x=k平行于y轴,分别与直线y=x、抛物线C交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,则满足条件的k为 如图,P是抛物线y=2x2上第一象限内的点,A点坐标为(6,0).
如图,P是抛物线y=2x2上第一象限内的点,A点坐标为(6,0). 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 如图,P是抛物线
如图,P是抛物线