题目内容
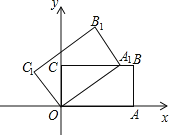
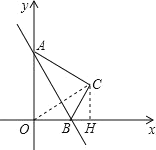
【题目】如图所示,在坐标平面内,点O是坐标原点,A(0,6)、B(2![]() ,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应。
,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应。
(1)求点C的坐标;
(2)动点F从点O出发,以2个单位长度/秒的速度沿折线O—A—C向终点C运动,设△FOB的面积为S(S≠0),点F的运动时间为t秒,求S与t的关系式,并直接写出t的取值范围;
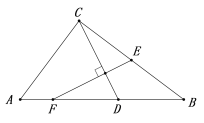
(3)在(2)的条件下,过点B作x轴垂线,交AC于点E,在点F的运动过程中,当t为何值时,△BEF是以BE为腰的等腰三角形?

【答案】(1)C(3![]() ,3);(2)当0<t3时,S=
,3);(2)当0<t3时,S=![]() ;当3<t6时,S=
;当3<t6时,S=![]() (3) t=1或t=3时,△BEF是以BE为腰的等腰三角形.
(3) t=1或t=3时,△BEF是以BE为腰的等腰三角形.
【解析】
(1)连接OC,过C点作CH⊥x轴于H点,易证△OAC是等边三角形,则OC=OA,在直角△OCH中,求得CH和OH,则C的坐标即可求得;
(2)分成当0<t≤3和3<t≤6两种情况,利用三角形的面积公式即可求解;
(3)分B是顶角顶点和E是顶角顶点两种情况进行讨论.
(1)连接OC,过C点作CH⊥x轴于H点
∵折叠△OAB,
∴OA=AC,∠OBA=∠CBA=60°,OB=CB,∠CBH=60°
∴△OAC是等边三角形
∴∠BCH=30°
∴BH=![]() BC=
BC=![]() ×2
×2![]() =
=![]() ,OH=2
,OH=2![]() +
+![]() =3
=3![]() ,
,
∵OC=OA=6,∠COH=30°
∴CH=![]() ×6=3.
×6=3.
∴C(3![]() ,3);
,3);
(2)当0<t3时:
OF=2t,S=![]() ;
;
当3<t6时:点F在AC上,
过点F作FG⊥y轴于G,连结OF,BF,
由运动知,AF=2t6,
由折叠知,∠OAC=2∠OAB=60°
∴AG=t3,OG=6(t3)=9t,
S=![]() OB×OG=
OB×OG=![]() =9
=9![]() -
-![]() t;
t;

(3)如图
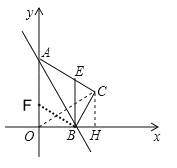
∵BE∥OA
∴∠ABE=∠OAB=30°
∴∠EBC=30°
∴CE=![]() BE,BE=AE
BE,BE=AE
∴BE=4.
当E是顶角顶点时,
∵∠ABE=30°,∠BAC=30°,则当F运动到A点时,△BEF为等腰三角形,即t=3;
当B是顶角顶点时,即BF=BE时,△BOF≌△BCE,
∴OF=CE=2
∴t=1.
此时,△BEF为等边三角形。
综上所述,t=1或t=3时,△BEF是以BE为腰的等腰三角形.

 一线名师提优试卷系列答案
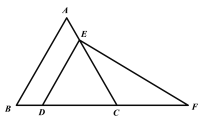
一线名师提优试卷系列答案【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
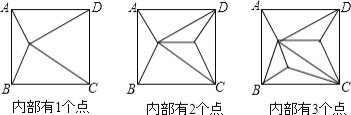
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.