��Ŀ����
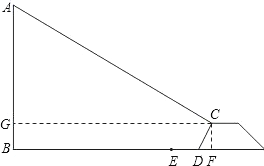
����Ŀ����ͼ��ijС���ڹ滮�����ڼ䣬�����С���㳡�ߵ�һ�����߸�AB����֪����߸�ABˮƽ����14�״��ǹ۾�̨����BD=14�ף��ù۾�̨������CD���½���CDF������ֵΪ2���۾�̨�ĸ�CFΪ2�ף����¶�C����õ��߸˶���A������Ϊ30�㣬D��E֮���ǿ�2�����е�������Ե�BΪԲ�ģ���AB��Ϊ�뾶��Բ������ΪΣ����������ͨ������˵���ڲ�����߸�ABʱ�����е��Ƿ���Σ�������ڣ���![]() ��1.73��
��1.73��
���𰸡�����Ҫ�����е�
��������
���������������֪�����õ�DF=1�ף�BG=2�ף��õ�BF=GC=15�ף���Rt��AGC�У���tan30��=![]() ���õ�AG=15��
���õ�AG=15��![]() =5
=5![]() ��5��1.732=8.660�ף����ǵõ����ۣ�
��5��1.732=8.660�ף����ǵõ����ۣ�
�⣺��tan��CDF=![]() =2��CF=2�ף�
=2��CF=2�ף�
��DF=1�ף�BG=2�ף�
��BD=14�ף�
��BF=GC=15�ף�
��Rt��AGC����tan30��=![]() ��
��
��AG=15��![]() =5
=5![]() ��5��1.732=8.660�ף�
��5��1.732=8.660�ף�
��AB=8.660+2=10.66�ף�
��BE=BD��ED=12�ף�
��BE��AB��
��˲���Ҫ�����е���

��ϰ��ϵ�д�
�����Ŀ