题目内容
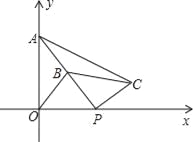
【题目】如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.
(1)判断△PBC的形状,并简要说明理由;
(2)当t>0时,试问:以P、O、B、C为顶点的四边形能否为平行四边形?若能,求出相应的t的值?若不能,请说明理由;
(3)当t为何值时,△AOP与△APC相似?
【答案】(1)等腰直角三角形(2)t=2(3)±1或±4
【解析】试题分析:(1)根据旋转的现在得出PB=PC,再根据B是线段PA的中点,得出∠BPC=90°,从而得出△PBC是等腰直角三角形.
(2)根据∠OBP=∠BPC=90°,得出OB∥PC,再根据B是PA的中点,得出四边形POBC是平行四边形,当OB⊥BP时,得出OP2=2OB2,即t2=2(![]() t2+1),求出符合题意的t的值,即可得出答案;
t2+1),求出符合题意的t的值,即可得出答案;
(3)根据题意得出∠AOP=∠APC=90°,再分两种情况讨论,当![]() 时和
时和![]() 时,得出△AOP∽△APC和△AOP∽△CPA,分别求出t的值即可.
时,得出△AOP∽△APC和△AOP∽△CPA,分别求出t的值即可.
试题解析:(1)△PBC是等腰直角三角形,理由如下:
∵线段PB绕着点P顺时针方向旋转90°,得到线段PC,
∴PB=PC,
∵B是线段PA的中点,
∴∠BPC=90°,
∴△PBC是等腰直角三角形.
(2)当OB⊥BP时,以P、O、B、C为顶点的四边形为平行四边形.
∵∠OBP=∠BPC=90°,
∴OB∥PC,
∵B是PA的中点,
∴OB=![]() AP=BP=PC,
AP=BP=PC,
∴四边形POBC是平行四边形,
当OB⊥BP时,有OP=![]() OB,即OP2=2OB2,
OB,即OP2=2OB2,
∴t2=2(![]() t2+1),
t2+1),
∴t1=2,t2=﹣2(不合题意),
∴当t=2时,以P、O、B、C为顶点的四边形为平行四边形.
(3)由题意可知,∠AOP=∠APC=90°,
当![]() 时,
时,
△AOP∽△APC,
此时OP=![]() OA=1,
OA=1,
∴t=±1,
当![]() 时,
时,
△AOP∽△CPA,
此时OP=2OA=4,
∴t=±4,
∴当t=±1或±4时,△AOP与△CPA相似.

 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案