题目内容
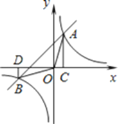
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交与
的图像交与![]() ,
,![]() 两点,过点A作
两点,过点A作![]() 轴于点C,过点B作
轴于点C,过点B作![]() 轴于点D,连接AO,
轴于点D,连接AO,![]() 得出以下结论:
得出以下结论:
①点A和点B关于直线![]() 对称;
对称;
②当![]() 时,
时,![]() ;
;
③![]() ;
;
④当![]() 时,
时,![]() ,
,![]() 都随x的增大而增大.
都随x的增大而增大.
其中正确的是![]()
A.①②③B.②③C.①③D.①②③④
【答案】A
【解析】
①先求出点A、B的坐标,再利用直线与直线的关系及点到直线的距离公式即可验证;②由①中A、B的坐标和函数图象可知;③由三角形面积公式即可验证;④观察直角坐标系和函数图象可知.
①将两个函数解析式联立,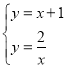 解得:
解得: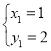 ,
,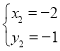
∴A(1,2),B(2,1),
∵AB所在直线![]() 的系数为1,直线
的系数为1,直线![]() 的系数为﹣1,
的系数为﹣1,
∴1×(﹣1)=﹣1即直线![]() 与直线
与直线![]() 垂直,
垂直,
又点A到直线![]() 的距离为:
的距离为: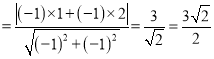
点B到直线![]() 的距离为:
的距离为: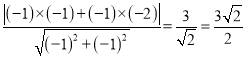 ,
,
即点A、B到直线![]() 的距离相等,
的距离相等,
∴A、B关于直线![]() 对称,故本项正确;
对称,故本项正确;
②由①中A、B的坐标和函数图象可知,当2<x<0或x>1时,一次函数的图象在反比例函数的上面,则y1>y2,故本项正确;
③∵S△AOC=![]() =1,S△BOD=
=1,S△BOD=![]() =1,
=1,
∴S△BOD=S△AOC,故本项正确;
④当x>0时,y1随x的增大而增大, y2随x的增大而减小,故本项错误;
综上,正确的是①②③.
故选:A

练习册系列答案
相关题目