题目内容
【题目】已知：如图，在四边形ABCD中，AD∥BC，连接对角线AC．
（1）在边AD上确定一点E，使EA=EC；在边BC上确定一点F，使FA=FC；（尺规作图，保留作图痕迹，不写作法）
（2）在（1）的条件下，连接AF，CE．求证：四边形AFCE是菱形．
【答案】（1）作图见解析；（2）证明见解析．
【解析】
（1）作线段AC的垂直平分线交AD于E，交BC于F，连接EC，AF即可；
（2）结合（1）证明AE＝EC＝CF＝AF，进而得证．
解：（1）如图，点E、F为所作；
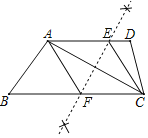
（2）∵EF垂直平分AC，
∴AE＝CE，AF＝CF，
∴EF平分∠AFC，即∠AFE＝∠CFE，
∵AD∥BC，
∴∠AEF＝∠CFE，
∴∠AFE＝∠AEF，
∴AE＝AF，
∴AE＝EC＝CF＝AF，
∴四边形AFCE为菱形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
