题目内容
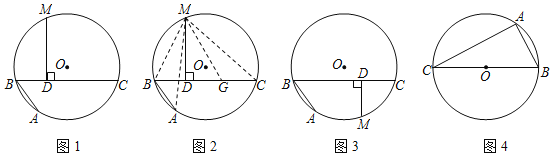
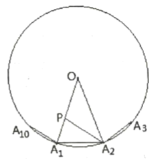
【题目】如图,![]() 是半径为1的
是半径为1的![]() 的内接正十边形,
的内接正十边形,![]() 平分
平分![]()
(1)求证:![]() ;
;
(2)求证:![]()
【答案】(1)详见解析;(2)详见解析
【解析】
(1)根据题意得出角相等得出△A1A2P∽△A1OA2,再根据相似三角形的性质即可得出答案;
(2)设A1A2=x,得出OP=PA2=A1A2=x,A1 P=1-x,再代入![]() 中即可求出答案.
中即可求出答案.
证明:(1)∵A1A2A3…A10是半径为1的⊙O的内接正十边形,A2P平分∠OA2A1
∴∠A1OA2=36°,∠A1=∠OA2A1=72°,∠A1A2P=∠O=36°
∴∠A1 P A2=72°,OP=PA2,
∴△A1A2P∽△A1OA2,![]()
∴A1A22=A1PO A1
(2)设A1A2=x,
则OP=PA2=A1A2=x,
∴A1 P=1-x,
由(1)得A1A22=A1PO A1
∴![]() ,
,
∴![]() ,
,
解得, (负值舍去)
(负值舍去)
∴![]() ,
,
即![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市水费采用阶梯收费制度,即:每月用水不超过15吨时,每吨需缴纳水费a元,每月用水量超过15吨时,超过15吨的部分按每吨提高b元缴纳下表是嘉琪家一至四月份用水量和缴纳水费情况.根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
月用水量(吨) | 14 | 18 | 16 | 13 |
水费(元) | 42 | 60 | 50 | 39 |
(1)a= 元;b= 元;
(2)求月缴纳水费p(元)与月用水量t(吨)之间的函数关系式;
(3)若嘉琪家五月和六月的月缴水费相差24元,求这两月用水量差的最小值.
【题目】某日王老师佩戴运动手环进行快走锻炼两次锻炼后数据如下表,与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的![]() 倍.设王老师第二次锻炼时平均步长减少的百分率为
倍.设王老师第二次锻炼时平均步长减少的百分率为![]() .注:步数
.注:步数![]() 平均步长
平均步长![]() 距离.
距离.
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) |
| ①_______ |
平均步长(米/步) |
| ②_______ |
距离(米) |
|
|
(1)根据题意完成表格;
(2)求![]() .
.
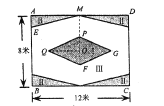
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,