题目内容
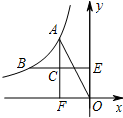 (2012•昌平区二模)如图,已知:反比例函数y=
(2012•昌平区二模)如图,已知:反比例函数y=| k | x |
(1)求反比例函数的解析式及m的值;
(2)若直线l过点O且平分△AFO的面积,求直线l的解析式.
分析:(1)先把A(-2,4)代入y=
可求出k=-8,则可确定反比例函数的解析式为y=-
,然后把B点坐标代入即可求出m的值;
(2)根据A、B两点坐标先求出C点坐标(-2,2),于是得到C点为AF的中点,则直线l过C点,然后利用待定系数法求出直线l的解析式.
| k |
| x |
| 8 |
| x |
(2)根据A、B两点坐标先求出C点坐标(-2,2),于是得到C点为AF的中点,则直线l过C点,然后利用待定系数法求出直线l的解析式.
解答: 解:(1)把A(-2,4)代入y=
解:(1)把A(-2,4)代入y=
得k=-2×4=-8,
∴反比例函数的解析式为y=-
,
把B(m,2)代入y=-
得,2m=-8,解得m=-4;
(2)∵A点坐标为(-2,4)、B点坐标为(-4,2),
而AF⊥x轴,BE⊥y轴,
∴C点坐标为(-2,2),
∴C点为AF的中点,
∵直线l过点O且平分△AFO的面积,
∴直线l过C点,
设直线l的解析式为y=kx(k≠0),
把C(-2,2)代入y=kx得2=-2k,解得k=-1,
∴直线l的解析式为y=-x.
 解:(1)把A(-2,4)代入y=
解:(1)把A(-2,4)代入y=| k |
| x |
∴反比例函数的解析式为y=-
| 8 |
| x |
把B(m,2)代入y=-
| 8 |
| x |
(2)∵A点坐标为(-2,4)、B点坐标为(-4,2),
而AF⊥x轴,BE⊥y轴,
∴C点坐标为(-2,2),
∴C点为AF的中点,
∵直线l过点O且平分△AFO的面积,
∴直线l过C点,
设直线l的解析式为y=kx(k≠0),
把C(-2,2)代入y=kx得2=-2k,解得k=-1,
∴直线l的解析式为y=-x.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
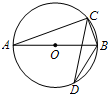 (2012•昌平区二模)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABC=70°,则∠BDC的度数为( )
(2012•昌平区二模)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABC=70°,则∠BDC的度数为( )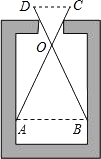 (2012•昌平区二模)如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC:OA=1:2,量得CD=10,则零件的内孔直径AB长为( )
(2012•昌平区二模)如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC:OA=1:2,量得CD=10,则零件的内孔直径AB长为( )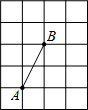 (2012•昌平区二模)如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是
(2012•昌平区二模)如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是