题目内容
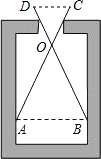（2012•昌平区二模）如图，用一个交叉卡钳（两条尺长AC和BD相等，OC=OD）量零件的内孔直径AB．若OC：OA=1：2，量得CD=10，则零件的内孔直径AB长为（ ）分析：要求零件的内孔直径AB长，由题可知只需求出AB即可．因为CD和AB平行，可得△AOB∽△COD，可以根据相似三角形对应边成比例即可解答．
解答：解：∵两条尺长AC和BD相等，OC=OD
∴OA=OB
∵OC：OA=1：2
∴OD：OB=OC：OA=1：2
∵∠COD=∠AOB
∴△AOB∽△COD
∴CD：AB=OC：OA=1：2
∵CD=10
∴AB=20
故选B．
∴OA=OB
∵OC：OA=1：2
∴OD：OB=OC：OA=1：2
∵∠COD=∠AOB
∴△AOB∽△COD
∴CD：AB=OC：OA=1：2
∵CD=10
∴AB=20
故选B．
点评：本题只要是把实际问题抽象到相似三角形中，利用相似三角形的相似比，求得AB的长即可．
练习册系列答案
相关题目
（2012•昌平区二模）如图，AB是⊙O的直径，C、D是⊙O上的两点，若∠ABC=70°，则∠BDC的度数为（ ）
（2012•昌平区二模）如图的方格纸中，每个小方格都是边长为1的正方形，A、B两点是方格纸中的两个格点，在4×5的方格纸中，找出格点C，使△ABC的面积为1个平方单位，则满足条件的格点C的个数是