��Ŀ����
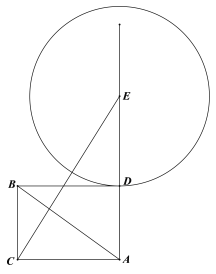
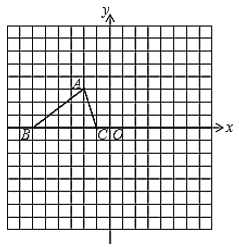
����Ŀ����ͼ����ABC�У���ACB=90����BC=6��AC=8����E���B��AC��ͬ�࣬��AE��AC��
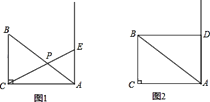
��1����ͼ1����E�����A�غϣ�����CE��AB�ڵ�P����AE=x��AP=y����y����x�ĺ�������ʽ��
��2���Ƿ���ڵ�E��ʹ��PAE���ABC���ƣ������ڣ���AE�ij����������ڣ�˵�����ɣ�
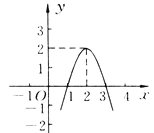
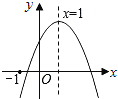
��3����ͼ2������B��BD��AE������ΪD�����Ե�EΪԲ�ģ�EDΪ�뾶��Բ��Ϊ��E������C����E�ϵ�ľ������СֵΪ8�����E�İ뾶��
���𰸡���1��![]() ����2��
����2��![]() ����3��9��
����3��9��![]() .
.
��������
��1�����ݹ��ɶ������AB�ij����ٸ��ݡ�APE�ס�BPC�ó�����ʽ������������������
��2�����ж�ֻ�С�EPA=90��ʱ����ʹ��PAE���ABC���ƣ���֤����ABC�ס�EAC����һ���������������ε����ʼ�����������
��3�����������жϵ�C���ڡ�E�ⲿ�����ǵ�C����E�ϵ�ľ������СֵΪCE��DE���ٷֵ�E���߶�AD�Ϻ��߶�AD���ӳ���������������ڡ�AEC�и��ݹ��ɶ����г�������⼴��.
�⣺��1����AE��AC����ACB=90����
��AE��BC��
���APE�ס�BPC��
��![]() ��
��
��BC=6��AC=8��
��AB=![]() =10��
=10��
��AE=x��AP=y��
��![]() ��
��
��![]() ��
��
��2���ߡ�ACB=90��������PAE���PEA������ǣ�
��Ҫʹ��PAE���ABC���ƣ�ֻ�С�EPA=90������CE��AB��
��ʱ��ABC�ס�ECA����![]() ����AE=
����AE=![]() ��
��
�ʴ��ڵ�E��ʹ��ABC�ס�EAP����ʱAE=![]() ��
��
��3���������֪��C���ڡ�E�ⲿ����ʱ��C����E�ϵ�ľ������СֵΪCE��DE��
��AE=x���ٵ���E���߶�AD��ʱ����ͼ��ED=6��x��EC=6��x+8=14��x��
����Rt��AEC�У����ݹ��ɶ�������x2+82=��14��x��2����ã�x=![]() ��
��
����E�İ뾶Ϊ![]() ��
��
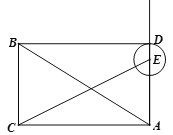
�ڵ���E���߶�AD�ӳ�����ʱ����ͼ��ED=x��6��EC=x��6+8=x+2��
����Rt��AEC�У����ݹ��ɶ�������x2+82=��x+2��2����ã�x=15������E�İ뾶Ϊ9��
���E�İ뾶Ϊ9��![]() ��
��