题目内容
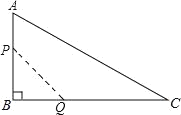
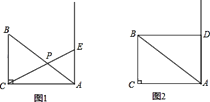
【题目】如图,□ABCD中,AB⊥AC,AB=1,BC=![]() .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
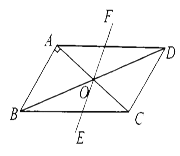
(1)试说明在旋转过程中,线段AF与EC总保持相等;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,请直接写出此时AC绕点O顺时针旋转的度数.
【答案】(1)AF=EC.(2)AC绕点O顺时针旋转45°时,四边形BEDF为菱形.
【解析】
试题(1)证明△AOF≌△COE即可;
(2)EF⊥BD时,四边形BEDF为菱形,可根据勾股定理求得AC=2,∴OA=1=AB,又AB⊥AC,∴∠AOB=45°.
试题解析:(1)证明:当∠AOF=90°时,
∵∠BAO=∠AOF=90°,
∴AB∥EF,
又∵AF∥BE,
∴四边形ABEF为平行四边形.
在△AOF和△COE中
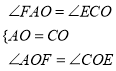 .
.
∴△AOF≌△COE(ASA).
∴AF=EC.
(2)解:四边形BEDF可以是菱形.
理由:如图,连接BF,DE
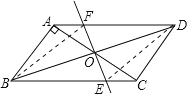
由(1)知△AOF≌△COE,得OE=OF,
∴EF与BD互相平分.
∴当EF⊥BD时,四边形BEDF为菱形.
在Rt△ABC中,AC=![]() ,
,
∴OA=1=AB,
又∵AB⊥AC,
∴∠AOB=45°,
∴∠AOF=45°,
∴AC绕点O顺时针旋转45°时,四边形BEDF为菱形.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目