题目内容
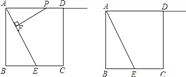
【题目】
、
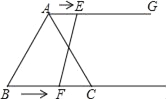
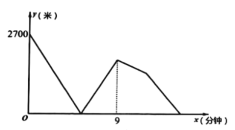
两地之间有一条直线跑道，甲，乙两人分别从、同时出发，相向而行均速跑步，且乙的速度是甲速度的80%，当甲，乙两人分别到达地，地后立即掉头往回跑，甲的速度保持不变，乙的速度提高25%（仍保持匀速前行）．甲，乙两人之间的距离
（米）与跑步时间
（分钟）之间的关系如图所示，则他们在第二次相遇时距地___________米．
【答案】1687.5
【解析】
观察函数图象，可知甲用9分钟到达B地，由速度=路程÷时间可求出甲的速度，结合甲、乙速度间的关系可求出乙的初始速度及乙加速后的速度，利用时间=路程÷速度可求出乙到达A地时的时间，设两人第二次相遇的时间为t分钟，由二者第二次相遇走过的总路程为A，B两点间距离的3倍，即可得出关于t的一元一次方程，解之即可得出t值，再利用甲、乙二人在第二次相遇时距B地的距离=甲的总路程-2700，即可求出结论．
甲的速度为2700÷9=300（米/分钟），
乙的初始速度为300×80%=240（米/分钟），
乙到达A地时的时间为2700÷240=
（分钟），
乙加速后的速度为240×（1+25%）=300（米/分钟）．
设两人第二次相遇的时间为t分钟，
根据题意得：300t+2700+300（t-）=2700×3，
解得：t=
，
∴他们在第二次相遇时距B地300t-2700=1687.5．
故答案为：1687.5
【题目】小华是花店的一名花艺师，她每天都要为花店制作普通花束和精致花束，她每月工作20天，每天工作8小时，她的工资由基本工资和提成工资两部分构成，每月的基本工资为l800元，另每制作一束普通花束可提2元，每制作一束精致花束可提5元．她制作两种花束的数量与所用时间的关系见下表：
制作普通花束（束） | 制作精致花束（束） | 所用时间（分钟） |
10 | 25 | 600 |
15 | 30 | 750 |
请根据以上信息，解答下列问题：
（1）小华每制作一束普通花束和每制作一束精致花束分别需要多少分钟？
（2）2019年11月花店老板要求小华本月制作普通花束的总时间
不少于3000分钟且不超过5000分钟，则小华该月收入
最多是多少元？此时小华本月制作普通花束和制作精致花束分别是多少束？
