题目内容
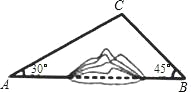
【题目】如图，A，B两地之间有一座山，汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC=10km，∠A=30°，∠B=45°，则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果精确到0.1km）（参考数据：
≈1.41，
≈1.73）
【答案】3.4
【解析】
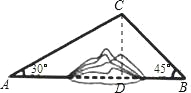
试题分析：过点C作AB的垂线CD，垂足为D，在直角△ACD和直角△CBD中，解直角三角形求出CD，AD，BC，就可以得到结论．
试题解析：过点C作AB的垂线CD，垂足为D．
∵AC=10km，∠A=30°，
∴CD=
AC=5（km）．
AD=
=5
（km）．
在Rt△CDB中，
∵∠B=45°，
∴CD=BD=5km．
∴BC=
=5
（km）．
∴从A地到B地汽车少走的距离是：AC+BC﹣AB．
即AC+BC﹣AB=AC+BC﹣（AD+BD）
=10+5﹣（5
+5）
=5×（1+﹣）
≈5×（1+1.41﹣1.73）
≈3.4（km）．
答：隧道开通后，汽车从A地到B地少走约3.4km．
练习册系列答案
阅读快车系列答案
相关题目
