题目内容
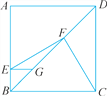
【题目】如图,在正方形ABCD中,点E,G分别在边AB,对角线BD上,EG∥AD,F为GD的中点,连结FC,请利用勾股定理的逆定理,证明EF⊥FC.
【答案】证明见解析
【解析】试题分析:作FH⊥AB于点H,延长HF交CD于点I,作FK⊥AD于点K,连接EC,则四边形FIDK是正方形,四边形AKFH是矩形,由EG∥AD,F为GD的中点,可得点H是AE的中点,进而可得:HE=AH=FK=DK=DI=FI,HF=BH=IC=AK,然后由勾股定理分别表示EF2,FC2,EC2,最后根据勾股定理的逆定理即可判断△EFC是直角三角形,进而可证EF⊥FC.
试题解析:如图,过点F作FH⊥AB于点H,FK⊥AD于点K,延长HF交CD于点I.由题意易得四边形FIDK是正方形,四边形AKFH是长方形,
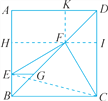
∴AK=HF,KD=DI=FI=KF=AH.
∵AD=CD,∴IC=AK=HF.
∵AD∥FH∥EG,F是DG的中点,
∴易证得HA=HE,∴HE=FI.
在Rt△HEF和Rt△FIC中,由勾股定理,得
EF2=HE2+HF2,FC2=FI2+IC2,
∴EF2+FC2=HE2+HF2+FI2+IC2=2HE2+2HF2.
在Rt△BCE中,由勾股定理,得
EC2=BE2+BC2.
∵BE2=(AB-AE)2=(AD-2HE)2
=(HF+FI-2HE)2=(HF+HE-2HE)2
=(HF-HE)2=HF2-2HF·HE+HE2,
BC2=(HF+FI)2=(HF+HE)2
=HF2+2HF·HE+HE2,
∴EC2=BE2+BC2=HF2-2HF·HE+HE2+HF2+2HF·HE+HE2
=2HE2+2HF2,
即EF2+FC2=EC2,
∴△EFC是直角三角形,且∠EFC=90°,
∴EF⊥FC.

练习册系列答案
相关题目