题目内容
【题目】观察如图所示的图形,并阅读相关文字信息后回答下列问题:
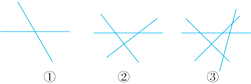
2条直线相交,最多有1个交点;3条直线相交,最多有3个交点;4条直线相交,最多有6个交点.
(1)8条直线相交,最多有几个交点?
(2)设有n条直线相交,最多有y个交点,请用含n的代数式表示y.
(3)当最多交点个数为4950时,此时直线有几条?
【答案】(1)28;(2)![]() ;(3)100
;(3)100
【解析】试题分析:先观察图形,找出交点的个数与直线的条数之间的关系,然后进行计算即可.
试题解析: (1)∵每增加一条直线,只要保证这条直线与原有的每一条直线都交于不同的点,就能使交点的个数最多,
∴当8条直线相交时,最多交点个数为1+2+3+4+5+6+7=28.
(2)y=1+2+3+…+(n-1)=![]() .
.
(3)当y=4950时,即![]() =4950,
=4950,
∴n(n-1)=9900=100×99,且n>0,
∴n=100,即此时直线有100条.

练习册系列答案
相关题目
【题目】列方程解应用题:某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的 ![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售.第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙种商品是按原价打几折销售?