题目内容
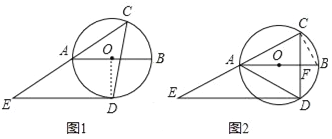
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是⊙O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

【答案】(1)证明见解析;
(2)S△ECD=![]() EDCD=
EDCD=![]() .
.
【解析】
试题分析:(1)如图1中,连接OD,欲证明ED是切线,只要证明∠EDO=90°即可.
(2)如图2中,连接BC,利用勾股定理.以及直角三角形30度性质求出CD、DE即可.
试题解析:(1)如图1中,连接OD.
∵∠C=45°,
∴∠AOD=2∠C=90°,
∵ED∥AB,
∴∠AOD+∠EDO=180°,
∴∠EDO=90°,
∴ED⊥OD,
∴ED是⊙O切线.
(2)如图2中,连接BC,
∵CF=DF,
∴AF⊥CD,
∴AC=AD,
∴∠ACD=∠ADC,
∵AB∥ED,
∴ED⊥DC,
∴∠EDC=90°,
在RT△ACB中,∵∠ACB=90°,∠CAB=30°,AB=2,
∴BC=1,AC=![]() ,
,
∴CF=![]() AC=
AC=![]() ,CD=2CF=
,CD=2CF=![]() ,
,
在RT△ECD中,
∵∠EDC=90°,CD=![]() ,∠E=∠CAB=30°,
,∠E=∠CAB=30°,
∴EC=2CD=2![]() ,ED=
,ED= ![]() =3,
=3,
∴S△ECD= ![]() EDCD=
EDCD=![]() .
.

练习册系列答案
相关题目