题目内容
【题目】如图，已知抛物线y=ax2+bx+1经过A（﹣1，0），B（1，1）两点．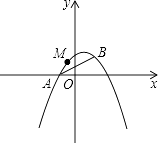
（1）求该抛物线的解析式；
（2）阅读理解：
在同一平面直角坐标系中，直线l1：y=k1x+b1（k1 ， b1为常数，且k1≠0），直线l2：y=k2x+b2（k2 ， b2为常数，且k2≠0），若l1⊥l2 ， 则k1k2=﹣1．
解决问题：
①若直线y=3x﹣1与直线y=mx+2互相垂直，求m的值；
②抛物线上是否存在点P，使得△PAB是以AB为直角边的直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）M是抛物线上一动点，且在直线AB的上方（不与A，B重合），求点M到直线AB的距离的最大值．
【答案】
（1）解：将A，B点坐标代入，得
，
解得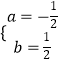 
，
抛物线的解析式为y=﹣ 
x2+ x+1；
（2）解：①由直线y=3x﹣1与直线y=mx+2互相垂直，得
3m=﹣1，
即m=﹣ 
；
②AB的解析式为y= x+ ，
当PA⊥AB时，PA的解析式为y=﹣2x﹣2，
联立PA与抛物线，得
，
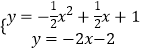解得 
（舍）， 
，即P（6，﹣14）；
当PB⊥AB时，PB的解析式为y=﹣2x+3，
联立PB与抛物线，得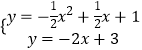 
，
解得 
（舍） 
即P（4，﹣5），
综上所述：△PAB是以AB为直角边的直角三角形，点P的坐标（6，﹣14）（4，﹣5）；
（3）解：如图
，
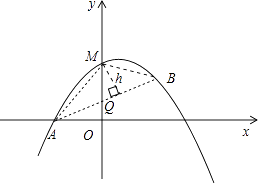∵M（t，﹣ t2+ t+1），Q（t， t+ ），
∴MQ=﹣ t2+
S△MAB= MQ|xB﹣xA
= （﹣ t2+ ）×2
=﹣ t2+ ，
当t=0时，S取最大值 ，即M（0，1）．
由勾股定理，得
AB= 
= 
，
设M到AB的距离为h，由三角形的面积，得
h= 
= 
．
点M到直线AB的距离的最大值是 ．
【解析】（1）利用待定系数法把A、B两点的坐标代入解析式即可求出a、b；（2）分类讨论，A或B为直角顶点两类，利用“阅读理解”的结论“相互垂直的直线的斜率k 乘积=-1”构建方程，求出直线解析式，再和抛物线联立方程组，得出交点即P坐标;（3）三角形的底边AB是定值，要求距离最大值就须求面积的最大值，须过M点作x轴的垂线，把三角形MAB分割成两个有竖直边的三角形，构建以M的横坐标t 为自变量的函数S,求出其最大值，再利用三角形面积公式，求出此时的点M到AB的距离，就是最大距离.
【考点精析】根据题目的已知条件，利用二次函数的最值的相关知识可以得到问题的答案，需要掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a．
