��Ŀ����
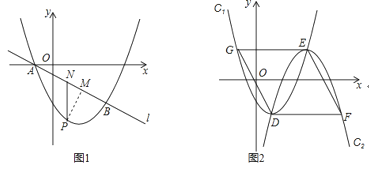
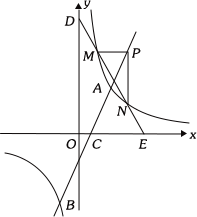
����Ŀ����ͼ��ֱ��y=ax+b(a��0)��˫����![]() (k��0)����һ���������ڵ�A��B������x�ύ�ڵ�C����A������Ϊ(2��m)����B������Ϊ(1��n)��cos��AOC=
(k��0)����һ���������ڵ�A��B������x�ύ�ڵ�C����A������Ϊ(2��m)����B������Ϊ(1��n)��cos��AOC=![]() .
.
(1)��÷�����������һ�κ����Ľ���ʽ��
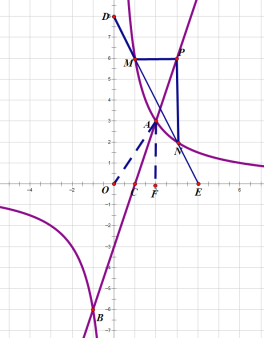
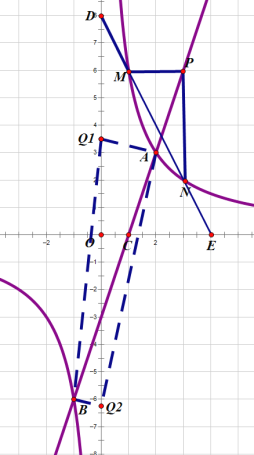
(2)��QΪy����һ�㣬��ABQ����ABΪֱ�DZߵ�ֱ�������Σ����Q�����ꣻ
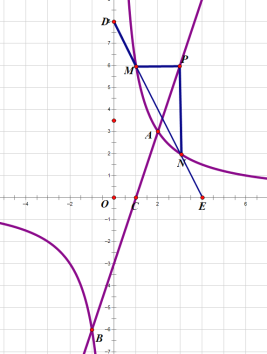
(3)��P(s��t)(s>2)��ֱ��AB���˶���PM��x�ύ˫������M��PN��y�ύ˫������N��ֱ��MN�ֱ�x�ᣬy����E��D����![]() ��ֵ.
��ֵ.
���𰸡���1��![]() ��
��![]() ��2��Q��0��
��2��Q��0��![]() ����0��
����0��![]() ����3��1
����3��1
��������
(1)����AO������![]() ����A������Ϊ2�����Եó���A�������꣬��A��������뷴���������Ϳɵó������ʽ,���A��B����ֱ����һ�κ��������һ�κ�������ʽ��
����A������Ϊ2�����Եó���A�������꣬��A��������뷴���������Ϳɵó������ʽ,���A��B����ֱ����һ�κ��������һ�κ�������ʽ��
(2)���ݵ�Q��y��������������������ȥ����ֱ�������ν����ڹ��ɶ��������Q���꼴�ɣ�
(3)�����������M��N������ֱ���s��t��ʾ��Ȼ�����PM��PN�ij�������![]() ���������.
���������.
�⣺(1)����AO������![]() ����A������Ϊ2��
����A������Ϊ2��
�ã�![]() ,��
,��![]() ,
,
����![]() ��������뷴��������ʽ
��������뷴��������ʽ
![]()
![]() ��������
��������![]() ��
��
��![]() ��
��![]() �������һ�κ�������ʽ��
�������һ�κ�������ʽ��![]()
![]() ����ã�
����ã�![]() ��
��
![]() .
.
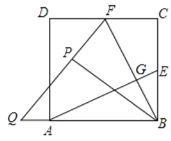
(2)��ͼ��ʾ��
�ٵ���![]() λ��y���������ʱ��
λ��y���������ʱ��
��ʱ![]()
����![]()
��ã�![]() ��
��
![]() ��
��
�ڵ���![]() λ��y�Ḻ�����ʱ��
λ��y�Ḻ�����ʱ��
��ʱ![]()
����![]()
��ã�![]() ��
��
![]() ��
��
�ۺϵã�![]() ��
��![]() .
.
(3)��������ɵã�![]() ��
��
��![]() ����
����![]() ��
��
������![]() ��
��![]() ��
��
![]() ��
��
����P��ֱ��![]() ������
������![]() ��
��
���߳���t�ã�![]() ��
��
�ۺ������ɵã�![]() ��
��
�ʴ�Ϊ��1

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�