题目内容
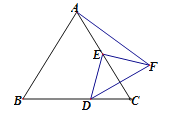
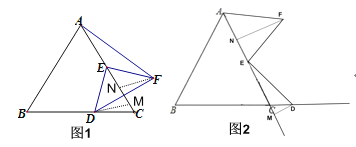
【题目】如图，△ABC是等边三角形，AB=4，E是AC的中点，D是直线BC上一动点，线段ED绕点E逆时针旋转90°，得到线段EF，当点D运动时，则AF的最小值为（ ）
A.2B.
C.
D.
【答案】D
【解析】
作DM⊥AC于M，FN⊥AC于N，设DM＝x，则CM＝
x，由旋转的性质易得△EDM≌△FEN，然后分D在BC上时和D在BC的延长线上时，分别通过勾股定理计算出AF2，然后利用二次函数的最值解答.
解：作DM⊥AC于M，FN⊥AC于N，
设DM＝x，
在Rt△CDM中，CM＝DM＝x，
∵线段ED绕点E逆时针旋转90°，得到线段EF，
∴ED＝EF，∠DEF＝90°，易得△EDM≌△FEN，
当D在BC上时，如图1，DM＝EN＝x，EM＝NF＝2x，
在Rt△AFN中，AF2＝(2x) 2＋(2+x)2＝
，
当D在BC的延长线上时，如图2，DM＝EN＝x，EM＝NF＝x＋2，
在Rt△AFN中，AF2＝(x+2) 2＋(2-x)2＝
，
当x＝
时，AF2有最小值
，
∵＞
∴AF的最小值为：
，
故选：D.
练习册系列答案
小学教材完全解读系列答案
相关题目
