��Ŀ����
����Ŀ��1.����ѧϰ.��֪![]() ����
����![]() Ϊ���ڲ�һ�㣬����
Ϊ���ڲ�һ�㣬����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �У��������һ�������Σ����ڽ���
�У��������һ�������Σ����ڽ���![]() �������ڽǷֱ���ȣ���ô�ͳƵ�
�������ڽǷֱ���ȣ���ô�ͳƵ�![]() Ϊ
Ϊ![]() �ĵȽǵ�.
�ĵȽǵ�.

2.����Ӧ��
(1)�ж��������������Ƿ�Ϊ����⣬��Ϊ�����⣬������Ӧ������д��������������֮����д����������.
���ڽǷֱ�Ϊ![]() ��
��![]() ��
��![]() �������δ��ڵȽǵ㣻 ��
�������δ��ڵȽǵ㣻 ��
������������ζ����ڵȽǵ�; ��
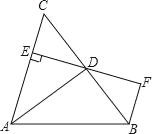
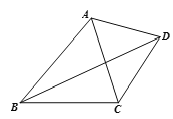
��2����ͼ�٣���![]() �����
�����![]() �ĵȽǵ㣬��
�ĵȽǵ㣬��![]() ��̽��ͼ���У�
��̽��ͼ���У�![]() ��
��![]() ��
��![]() ֮���������ϵ����˵������.
֮���������ϵ����˵������.
3.�������
��ͼ�ڣ���![]() �У�
��![]() ����
����![]() �������ڽǵĽ�ƽ���ߵĽ���
�������ڽǵĽ�ƽ���ߵĽ���![]() �Ǹ������εĵȽǵ㣬��
�Ǹ������εĵȽǵ㣬��![]() �����������ڽǵĶ���.
�����������ڽǵĶ���.
���𰸡���1���棬�٣���2����BPC����ABC����ACP��֤����������3��![]() ��
��![]() ��
��![]() ��
��
��������
��1�����ݵȽǵ�Ķ��壬��֪�ڽǷֱ�Ϊ30��60��90�������δ��ڵȽǵ㣬���ȱ������β����ڵȽǵ㣬�ݴ��жϼ��ɣ�
��2�����ݡ�ABC�У���BPC����ABP����BAC����ACP�Լ���BAC����PBC�����Ƶ������ɵó���BPC����ABC����ACP֮���������ϵ��
��3�����ݡ�ABC�������ڽǵĽ�ƽ���ߵĽ���P�Ǹ������εĵȽǵ㣬�Լ��������ڽǺ�Ϊ180�㣬�ó����ڡ�A�ķ��̣���á�A�Ķ������ó��������������ڽǵĶ�����
�⣺��1�����ڽǷֱ�Ϊ30��60��90�������δ��ڵȽǵ��������⣻
������������ζ����ڵȽǵ��Ǽ����⣬��ȱ������β����ڵȽǵ㣻
�ʴ�Ϊ���棬�٣�
��2����BPC����ABC����ACP���������£�
��ͼ�٣�
���ڡ�ABC�У���BPC����ABP����BAC����ACP����BAC����PBC��
���BPC����ABP����PBC����ACP����ABC����ACP��
��3����PΪ��ABC�Ľ�ƽ���ߵĽ��㣬
���PBC��![]() ��ABC����PCB��
��ABC����PCB��![]() ��ACB��
��ACB��
��PΪ��ABC�ĵȽǵ㣬
���PBC����BAC����BCP����ABC��2��PBC��2��BAC����ACB����BPC��4��A��
�֡ߡ�A����ABC����ACB��180�㣬
���A��2��A��4��A��180�㣬
���A��![]() ��
��
��������������ڽǵĶ����ֱ�Ϊ![]()
![]()
![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�