题目内容
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.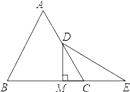
(1)求∠E的度数.
(2)求证:M是BE的中点.
【答案】
(1)解:∵三角形ABC是等边△ABC,
∴∠ACB=∠ABC=60°,
又∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE,
∴∠E= ![]() ∠ACB=30°;
∠ACB=30°;
(2)证明:连接BD,

∵等边△ABC中,D是AC的中点,
∴∠DBC= ![]() ∠ABC=
∠ABC= ![]() ×60°=30°
×60°=30°
由(1)知∠E=30°
∴∠DBC=∠E=30°
∴DB=DE
又∵DM⊥BC
∴M是BE的中点.
【解析】(1)根据等边三角形的性质得出∠ACB的度数,由CE=CD得出∠E=∠CDE,再根据三角形的一个外角等于和它不相邻的两内角之和,求出∠E的度数。
(2)抓住已知条件等边△ABC中,D是AC的中点,由等腰三角形的三线合一的性质,可知应连接BD,得出BD平分∠ABC,求出∠DBC的度数,继而证得DB=DE,再根据等腰三角形的性质即可证得结论。
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目

