题目内容
【题目】对于给定的![]() ,我们给出如下定义:若点M是边
,我们给出如下定义:若点M是边![]() 上的一个定点,且以M为圆心的半圆上的所有点都在
上的一个定点,且以M为圆心的半圆上的所有点都在![]() 的内部或边上,则称这样的半圆为
的内部或边上,则称这样的半圆为![]() 边上的点M关于
边上的点M关于![]() 的内半圆,并将半径最大的内半圆称为点M关于
的内半圆,并将半径最大的内半圆称为点M关于![]() 的最大内半圆.若点M是边
的最大内半圆.若点M是边![]() 上的一个动点(M不与B,C重合),则在所有的点M关于
上的一个动点(M不与B,C重合),则在所有的点M关于![]() 的最大内半圆中,将半径最大的内半圆称为
的最大内半圆中,将半径最大的内半圆称为![]() 关于
关于![]() 的内半圆.
的内半圆.
(1)在![]() 中,
中,![]() ,
,![]() ,
,
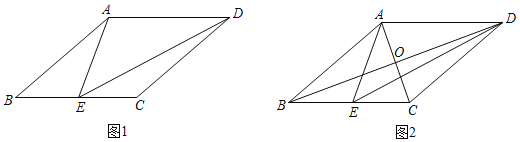
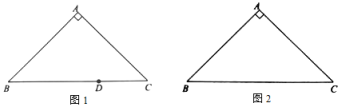
①如图1,点D在边![]() 上,且
上,且![]() ,直接写出点D关于
,直接写出点D关于![]() 的最大内半圆的半径长;
的最大内半圆的半径长;
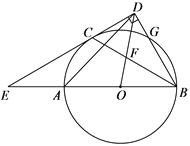
②如图2,画出![]() 关于
关于![]() 的内半圆,并直接写出它的半径长;
的内半圆,并直接写出它的半径长;
(2)在平面直角坐标系![]() 中,点E的坐标为
中,点E的坐标为![]() ,点P在直线
,点P在直线![]() 上运动(P不与O重合),将
上运动(P不与O重合),将![]() 关于
关于![]() 的内半圆半径记为R,当
的内半圆半径记为R,当![]() 时,求点P的横坐标t的取值范围.
时,求点P的横坐标t的取值范围.
【答案】(1)①![]() ,②1,作图见详解;(2)t≥
,②1,作图见详解;(2)t≥![]() 或
或![]() .
.
【解析】
(1)①过点D作DE⊥AC,则以点D为圆心,DE长为半径的半圆与AC相切,利用等腰直角三角形的性质,即可求解;
②当点D为BC的中点时,以D为圆心,DE为半径的半圆就是![]() 关于
关于![]() 的内半圆,进而可求解;
的内半圆,进而可求解;
(2)设点P坐标为(t,![]() ),分两种情况分类讨论,①点P在第一象限时,②点P在第三象限时,分别求出t的取值范围,即可.
),分两种情况分类讨论,①点P在第一象限时,②点P在第三象限时,分别求出t的取值范围,即可.
(1)①如图1,过点D作DE⊥AC,则以点D为圆心,DE长为半径的半圆与AC相切,
∴D关于![]() 的最大内半圆的半径长就是DE的长,
的最大内半圆的半径长就是DE的长,
∵在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴DE=CD÷![]() =1÷
=1÷![]() =
=![]()
②如图2,当点D为BC的中点时,以D为圆心,DE为半径的半圆就是![]() 关于
关于![]() 的内半圆,
的内半圆,
∵在![]() 中,
中,![]() ,
,![]() ,DE⊥AC ,
,DE⊥AC ,
∴DE∥BA,
∴DE=![]() =
=![]() ×2=1;
×2=1;
(2)∵点P在直线![]() 上,
上,
∴∠POE=30°
设点P坐标为(t,![]() ),
),
∵点E的坐标为![]() ,
,
∴OE=3,
①若点P在第一象限时,设点M是线段OE上的动点,作MN⊥OP,MG⊥PE,
∵![]() ,
,
∴当R=![]() 时,如图3,则MN=MG=
时,如图3,则MN=MG=![]() ,OM=2×MN==2×
,OM=2×MN==2×![]() =
=![]() ,
,
∴ME=3-![]() =
=![]() ,
,
∴OM=ME,
在RtOMN和RtEMG中,
∵![]()
∴RtOMN RtEMG(HL)
∴∠MON=∠MEG=30°,
∴点P的横坐标t=![]() ,
,
当R=1时,如图4,则MN=1,OM=2×MN==2×1=2,此时,点P的横坐标t≥3,
∴t≥![]() 时,
时,![]() ;
;
②若点P在第三象限时,作 MG⊥PE,PH⊥x轴,
当R=![]() 时,如图5,则MG=MO=
时,如图5,则MG=MO=![]() ,
,
∴ME=3-MO=3-![]() =
=![]() ,
,
∴EG=![]() ,
,
∴tanE=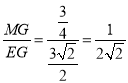 ,
,
∴![]() ,
,
∴ ,解得:
,解得:![]() ,
,
∴![]() 时,
时,![]() .
.
综上所述:t≥![]() 或
或![]() .
.
图1 图2
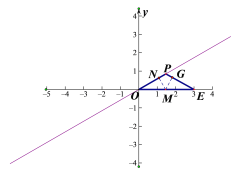

图3 图4
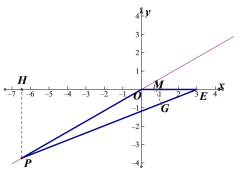
图5