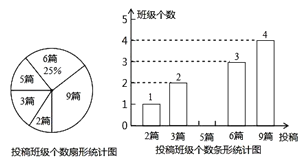
题目内容
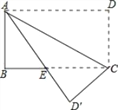
【题目】如图,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.
【答案】![]()
【解析】试题分析:根据矩形性质得AB=DC=6,BC=AD=8,AD∥BC,∠B=90°,再根据折叠性质得∠DAC=∠D′AC,而∠DAC=∠ACB,则∠D′AC=∠ACB,所以AE=EC,设BE=x,则EC=4-x,AE=4-x,然后在Rt△ABE中利用勾股定理可计算出BE的长即可.
试题解析:∵四边形ABCD为矩形,
∴AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,
∵△ACD沿AC折叠到△ACD′,AD′与BC交于点E,
∴∠DAC=∠D′AC,
∵AD∥BC,∴∠DAC=∠ACB,
∴∠D′AC=∠ACB,∴AE=EC,
设BE=x,则EC=4﹣x,AE=4﹣x,
在Rt△ABE中,∵AB2+BE2=AE2,
∴32+x2=(4﹣x)2,解得x=![]() ,
,
即BE的长为![]() .
.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目