题目内容
已知二次函数y=x2+bx+c图象的对称轴是直线x=2,且过点A(0,3).(1)求b、c的值;
(2)求出该二次函数图象与x轴的交点B、C的坐标;
(3)如果某个一次函数图象经过坐标原点O和该二次函数图象的顶点M.问在这个一次函数图象上是否存在点P,使得△PBC是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)把点A的坐标和对称轴代入即可;
(2)把y=0代入解一元二次方程即可;
(3)根据直角三角形的性质,设P点的坐标是(x,-
x),由勾股定理即可求出Q、H的坐标;把x=1或3代入即可求出另外的坐标.
(2)把y=0代入解一元二次方程即可;
(3)根据直角三角形的性质,设P点的坐标是(x,-
| 1 |
| 2 |
解答:解:(1)二次函数y=x2+bx+c图象的对称轴是直线x=2,且过点A(0,3),
代入得:-
=2,3=c,
解得:b=-4,c=3,
答:b=-4,c=3.
(2)把b=-4,c=3代入得:y=x2-4x+3,
当y=0时,x2-4x+3=0,
解得:x1=3,x2=1,
B?(3,0),C(1,0),
答:二次函数图象与x轴的交点B、C的坐标分别是(3,0),(1,0).
(3)存在: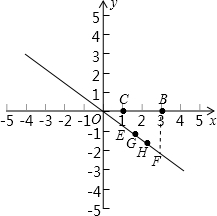
理由是:y=x2-4x+3,
=(x-2)2-1,
顶点坐标是(2,-1),
设一次函数的解析式是y=kx+b,
把(0,0),(2,-1)代入得:
,
解得:
,
∴y=-
x,
设P点的坐标是(x,-
x),
取BC的中点M,以M为圆心,以BM为半径画弧交直线于Q、H,
则Q、H符合条件,由勾股定理得;
(x-2)2+(-
x-0)2=12,
解得:x1=
,x2=2,
∴Q(
,-
),H(2,-1);
过B作BF⊥X轴交直线于F,
把x=3代入y=-
x得:y=-
,
∴F(3,-
),
过C作CE⊥X轴交直线于E,
同法可求:E(1,-
),
∴P的坐标是(
,-
)或(2,-1)或(3,-
)或(1,-
).
答:存在,P的坐标是(
,-
)或(2,-1)或(3,-
)或(1,-
).
代入得:-
| b |
| 2×1 |
解得:b=-4,c=3,
答:b=-4,c=3.
(2)把b=-4,c=3代入得:y=x2-4x+3,
当y=0时,x2-4x+3=0,
解得:x1=3,x2=1,
B?(3,0),C(1,0),
答:二次函数图象与x轴的交点B、C的坐标分别是(3,0),(1,0).
(3)存在:

理由是:y=x2-4x+3,
=(x-2)2-1,
顶点坐标是(2,-1),
设一次函数的解析式是y=kx+b,
把(0,0),(2,-1)代入得:
|
解得:
|
∴y=-
| 1 |
| 2 |
设P点的坐标是(x,-
| 1 |
| 2 |
取BC的中点M,以M为圆心,以BM为半径画弧交直线于Q、H,
则Q、H符合条件,由勾股定理得;
(x-2)2+(-
| 1 |
| 2 |
解得:x1=
| 6 |
| 5 |
∴Q(
| 6 |
| 5 |
| 3 |
| 5 |
过B作BF⊥X轴交直线于F,
把x=3代入y=-
| 1 |
| 2 |
| 3 |
| 2 |
∴F(3,-
| 3 |
| 2 |
过C作CE⊥X轴交直线于E,
同法可求:E(1,-
| 1 |
| 2 |
∴P的坐标是(
| 6 |
| 5 |
| 3 |
| 5 |
| 3 |
| 2 |
| 1 |
| 2 |
答:存在,P的坐标是(
| 6 |
| 5 |
| 3 |
| 5 |
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了二次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,直角三角形斜边上中线等知识点,解此题的关键是求出点P的坐标,此题难度较大.用的数学思想是分类讨论思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知二次函数y=x2+(2a+1)x+a2-1的最小值为0,则a的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
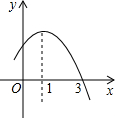 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )| A、x1=1,x2=3 | B、x1=0,x2=3 | C、x1=-1,x2=1 | D、x1=-1,x2=3 |
 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).