Question

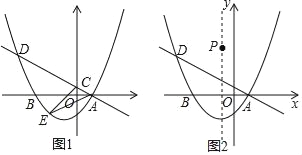
【题目】如图，抛物线y＝﹣(x+1)(x﹣3)与x轴分别交于点A、B(点A在B的右侧)，与y轴交于点C，⊙P是△ABC的外接圆．

(1)直接写出点A、B、C的坐标及抛物线的对称轴；

(2)求⊙P的半径；

(3)点D在抛物线的对称轴上，且∠BDC＞90°，求点D纵坐标的取值范围；

(4)E是线段CO上的一个动点，将线段AE绕点A逆时针旋转45°得线段AF，求线段OF的最小值．

Answer 1

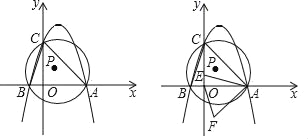
【答案】(1)点B的坐标为(﹣1，0)，点A的坐标为(3，0)，点C的坐标为(0，3)；抛物线的对称轴为直线x＝1；(2)⊙P的半径为；(3)1＜y＜2；(4)3﹣．

【解析】

(1)分别代入y＝0、x＝0求出与之对应的x、y的值，进而可得出点A、B、C的坐标，再由二次函数的对称性可找出抛物线的对称轴；

(2)连接CP、BP，在Rt△BOC中利用勾股定理可求出BC的长，由等腰直角三角形的性质及圆周角定理可得出∠BPC＝90°，再利用等腰直角三角形的性质可求出BP的值即可；

(3)设点D的坐标为(1，y)，当∠BDC＝90°时，利用勾股定理可求出y值，进而可得出：当1＜y＜2时，∠BDC＞90°；

(4)将△ACO绕点A逆时针方向旋转45°，点C落在点C′处，点O落在点O′处，根据旋转的性质可找出点C′的坐标及∠AC′O′＝45°，进而可找出线段C′O′所在直线的解析式，由点E在CO上可得出点F在C′O′上，过点O作OF⊥C′O′于点F，则△OC′F为等腰直角三角形，此时线段OF取最小值，利用等腰直角三角形的性质即可求出此时OF的长即可.

(1)当y＝0时，﹣(x+1)(x﹣3)＝0，

解得：x1＝﹣1，x2＝3，

∴点B的坐标为(﹣1，0)，点A的坐标为(3，0)；

当x＝0时，y＝﹣(0+1)×(0﹣3)＝3，

∴点C的坐标为(0，3)；

∵抛物线与x轴交于点(﹣1，0)、(3，0)，

∴抛物线的对称轴为直线x＝1；

(2)连接CP、BP，如图1所示，

在Rt△BOC中，BC＝,

∵∠AOC＝90°，OA＝OC＝3，

∴∠OAC＝∠OCA＝45°，

∴∠BPC＝2∠OAC＝90°，

∴CP＝BP＝BC＝，

∴⊙P的半径为；

(3)设点D的坐标为(1，y)，当∠BDC＝90°时，BD2+CD2＝BC2，

∴[(﹣1﹣1)2+(0﹣y)2]+[(0﹣1)2+(3﹣y)2]＝10，

整理，得：y2﹣3y+2＝0，

解得：y1＝1，y2＝2，

∴当1＜y＜2时，∠BDC＞90°；

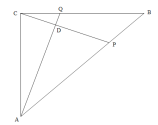
(4)将△ACO绕点A逆时针方向旋转45°，点C落在点C′处，点O落在点O′处，如图2所示．

∵AC＝，∠ACO＝45°，

∴点C′的坐标为(3﹣3，0)，∠AC′O′＝45°，

∴线段C′O′所在直线的解析式为y＝﹣x+3﹣3，

∵点E在线段CO上，

∴点F在线段C′O′上．

过点O作OF⊥C′O′于点F，则△OC′F为等腰直角三角形，此时线段OF取最小值，

∵△OC′F为等腰直角三角形，

∴OF＝OC′＝(3﹣3)＝3﹣．