��Ŀ����
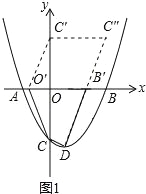
����Ŀ����ͼ1����֪������y=![]() x2��
x2��![]() x��3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD
x��3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD

��1�������A��B��D�����ꣻ
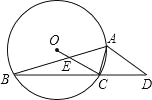
��2����ͼ1�����߶�OB��x�����ƶ����ҵ�O��B�ƶ���Ķ�Ӧ��ΪO����B������β˳�����ӵ�O����B����D��C�����ı���O��B��DC��������ı���O��B��DC���ܳ���Сֵ��
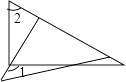
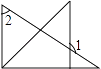
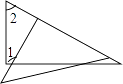
��3����ͼ2������M����������һ�㣬��N��y���ϣ�����CM��MN������CMN����MNΪֱ�DZߵĵ���ֱ��������ʱ��ֱ��д����N�����꣮
���𰸡���1��A����2��0����B��4��0����D��1����![]() ������2��4+
������2��4+![]() +
+![]() ����3��N��������0��
����3��N��������0��![]() ������0��
������0��![]() ������0����
������0����![]() ����0����
����0����![]() ����
����
��������
�����������1���������߽���ʽ��y=0�������x��һԪ���η��̼��������A��B�����꣬�������䷽���������߽���ʽ�����䷽���ɵó�����D�����ꣻ��2������C��0����3������x��ĶԳƵ�C����0��3��������C����0��3������ƽ��4����λ�õ���C����4��3��������DC������x���ڵ�B��������B������ƽ��4����λ�õ���O��������CO����CO�������ı���O��B��C��C��Ϊƽ���ı��Σ���ʱ�ı���O��B��DC�ܳ�ȡ��Сֵ���ٸ��������ľ��빫ʽ���CD��DC���ij��ȣ����ɵó����ۣ���3������M��λ�ò�ͬ������������ǣ�����M��ֱ��y=x��3�ϣ�����ֱ���������߽���ʽ�����M�����꣬��ϵ�C�������Լ�����ֱ�������ε����ʼ��ɵó���N�����ꣻ����M��ֱ��y=��x��3�ϣ�����ֱ���������߽���ʽ�����M�����꣬��ϵ�C�������Լ�����ֱ�������ε����ʼ��ɵó���N�����꣮�ۺ�����������ɵó����ۣ�
�����������1����y=![]() x2��
x2��![]() x��3��y=0����
x��3��y=0����![]() x2��
x2��![]() x��3=0����ã�x1=��2��x2=4����A����2��0����B��4��0������y=
x��3=0����ã�x1=��2��x2=4����A����2��0����B��4��0������y=![]() x2��
x2��![]() x��3=
x��3=![]() ��x2��2x����3=
��x2��2x����3=![]() ��x��1��2��
��x��1��2��![]() ����D��1����
����D��1����![]() ������2����y=
������2����y=![]() x2��
x2��![]() x��3��x=0����y=��3����C��0����3����D��1����
x��3��x=0����y=��3����C��0����3����D��1����![]() ����O��B��=OB=4����ͼ1��
����O��B��=OB=4����ͼ1��
����C��0����3������x��ĶԳƵ�C����0��3��������C����0��3������ƽ��4����λ�õ���C����4��3��������DC������x���ڵ�B��������B������ƽ��4����λ�õ���O��������CO����C��O�������ı���O��B��C��C��Ϊƽ���ı��Σ���ʱ�ı���O��B��DC�ܳ�ȡ��Сֵ����ʱC�ı���O��B��DC=CD+O��B��+CO��+DB��=CD+O��B��+DC������O��B��=4��CD=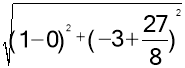 =
=![]() ��C��D=
��C��D=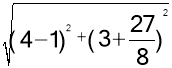 =
=![]() �����ı���O��B��DC���ܳ���СֵΪ4+
�����ı���O��B��DC���ܳ���СֵΪ4+![]() +
+![]() ����3����CMN����MNΪֱ�DZߵĵ���ֱ�������η������������ͼ2����
����3����CMN����MNΪֱ�DZߵĵ���ֱ�������η������������ͼ2����
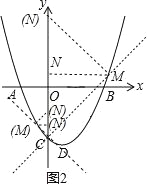 ��������C��ֱ��y=x��3���������ڵ�M������ֱ��CM�������ߵĽ���ʽ�ã�
��������C��ֱ��y=x��3���������ڵ�M������ֱ��CM�������ߵĽ���ʽ�ã�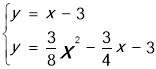 ����ã�
����ã�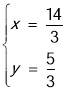 ��
��![]() ����ȥ������M��
����ȥ������M��![]() ��
��![]() �����ߡ�CMNΪ����ֱ�������Σ�C��0����3��������N������Ϊ��0��
�����ߡ�CMNΪ����ֱ�������Σ�C��0����3��������N������Ϊ��0��![]() ����0��
����0��![]() ����������C��ֱ��y=��x��3���������ڵ�M������ֱ��CM�������ߵĽ���ʽ�ã�
����������C��ֱ��y=��x��3���������ڵ�M������ֱ��CM�������ߵĽ���ʽ�ã�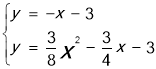 ����ã�
����ã�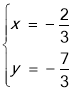 ��
��![]() ����ȥ������M����
����ȥ������M����![]() ����
����![]() �����ߡ�CMNΪ����ֱ�������Σ�C��0����3��������N������Ϊ��0����
�����ߡ�CMNΪ����ֱ�������Σ�C��0����3��������N������Ϊ��0����![]() ����0����
����0����![]() �������Ͽ�֪������CMN����MNΪֱ�DZߵĵ���ֱ��������ʱ����N������Ϊ��0��
�������Ͽ�֪������CMN����MNΪֱ�DZߵĵ���ֱ��������ʱ����N������Ϊ��0��![]() ������0��
������0��![]() ������0����
������0����![]() ����0����
����0����![]() ����
����

 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�