题目内容
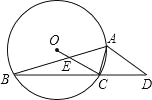
【题目】如图所示，⊙O的内接△ABC中，∠BAC=45°，∠ABC=15°，AD∥OC并交BC的延长线于D点，OC交AB于E点．
（1）求∠D的度数；
（2）求证：AC2=ADCE．
【答案】（1）45°；（2）证明参见解析.
【解析】
试题分析：（1）连接OA，由圆周角∠ABC与圆心角∠AOC所对的弧为同一条弧，根据同弧所对的圆心角等于所对圆周角的2倍，由∠ABC的度数求出∠AOC的度数，再由OA=OC，根据等边对等角，由顶角∠AOC的度数，利用三角形的内角和定理求出底角∠ACO的度数，再由∠BAC及∠ABC的度数，求出∠ACB的度数，由∠ACB﹣∠ACO求出∠BCE的度数，由OC与AD平行，根据两直线平行同位角相等可得∠D=∠BCE，可得出∠D的度数；（2）由∠ACB的度数，利用邻补角定义求出∠ACD的度数，再由∠AEC为三角形BEC的外角，利用外角性质得到∠AEC=∠ABC+∠BCE，可得出∠AEC的度数，进而得到∠AEC=∠ACD，在三角形ACD中，由∠ACD及∠D的度数，求出∠CAD的度数，可得∠CAD=∠ACE，利用两对对应角相等的三角形相似可得三角形AEC与三角形DCA相似，根据相似三角形的对应边成比例可得证．
试题解析：（1）连接OA，如图所示：
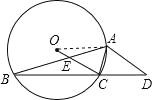
∵圆周角∠ABC与圆心角∠AOC所对的弧都为弧AC，∴∠AOC=2∠ABC，又∠ABC=15°，∴∠AOC=30°，又OA=OC，∴∠OAC=∠OCA=
=75°，又∠BAC=45°，∠ABC=15°，∴∠ACB=120°，∴∠OCB=∠ACB﹣∠ACO=120°﹣75°=45°，又OC∥AD，∴∠D=∠OCB=45°；（2）∵∠ABC=15°，∠OCB=45°，∴∠AEC=60°，又∠ACB=120°∴∠ACD=60°，∴∠AEC=∠ACD=60°，∵∠D=45°，∠ACD=60°，∴∠CAD=75°，又∠OCA=75°，∴∠CAD=∠OCA=75°，∴△ACE∽△DAC，∴
=
，即AC2=ADCE．
