题目内容
【题目】在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)如图1,求证:四边形![]() 是菱形;
是菱形;

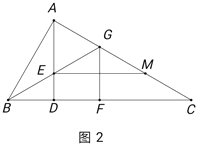
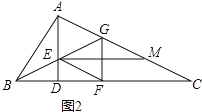
(2)如图2,若![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,在不添加任何辅助线的情况下,请直接写出图2中是
,在不添加任何辅助线的情况下,请直接写出图2中是![]() 长
长![]() 倍的所有线段.
倍的所有线段.
【答案】(1)证明见解析;(2)AB、BF、CF、EM.
【解析】
(1)先证明四边形AEFG是平行四边形,再证明AE=AG即可;
(2)先证明AB=![]() AG,再分别证明AB=BF=CF=EM,CM=AG即可.
AG,再分别证明AB=BF=CF=EM,CM=AG即可.
解:(1)∵AD⊥BC,GF⊥BC,

∴∠ADF=∠GFC=90°,
∴AE∥GF,
在△ABG和△FBG中, ,
,
∴△ABG≌△FBG,
∴AG=FG,
∵∠FBG+∠BED=90°,
∵∠BED=∠AEG,
∴∠FBG+∠AEG=90°,
∵∠ABG+∠AGE=90°,
∵∠ABG=∠FBG,
∴∠AEG=∠AGE,
∴AE=AG,
∴AE=FG,
∴四边形AEFG是平行四边形,
∵AE=AG∴四边形AEFG是菱形.
(2)∵四边形AEFG是菱形,
∴AE=AG,
∵BE=EG,∠BAG=90°,
∴AE=BE=EG,
∴△AEG是等边三角形,
∴∠AGE=60°,
在RT△ABG中,∵∠ABG=30°,
∴AB=![]() AG,
AG,
∵∠C=30°,∴BC=2AB,
∴BE=GE,EF∥AC,EM∥BC,
∴BF=FC,CM=GM,
在RT△AEM中,∵∠AME=∠C=30°,∠GEM+∠GME=60°,
∴∠GEM=∠GME=30°,
∴EG=AG=GM=CM,
∵EM∥FC,EF∥CM,
∴四边形EFCM是平行四边形,
∴AB=BF=CF=EM=![]() CM,
CM,
∴是CM长![]() 倍的所有线段有AB、BF、CF、EM.
倍的所有线段有AB、BF、CF、EM.

练习册系列答案
相关题目








