题目内容
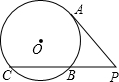 如图:PA切⊙O于点A,PBC是⊙O的一条割线,且PA=3
如图:PA切⊙O于点A,PBC是⊙O的一条割线,且PA=3| 3 |
A、
| ||||
B、3
| ||||
C、
| ||||
| D、2 |
分析:设PB=BC=x,利用切割线定理,可得关于x的方程,解出即可.
解答:解:设PB=BC=x,根据题意得
PA2=PB•PC,
∴PA2=PB(PB+BC),
∴(3
)2=x•2x,
解得x=
,
即BC=
.
故选A.
PA2=PB•PC,
∴PA2=PB(PB+BC),
∴(3
| 3 |
解得x=
| 3 |
| 2 |
| 6 |
即BC=
| 3 |
| 2 |
| 6 |
故选A.
点评:本题主要考查圆的切割线定理,即:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.

练习册系列答案
相关题目
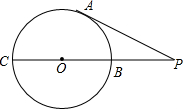 如图,PA切⊙O于点A,PC过点O且于点B、C,若PA=6cm,PB=4cm,则⊙O的半径为
如图,PA切⊙O于点A,PC过点O且于点B、C,若PA=6cm,PB=4cm,则⊙O的半径为 21、如图,PA切⊙O于点A,割线PBC交⊙O于B、C两点,∠APC的平分线分别交AC、AB于D、E两点.请在图中找出2对相似三角形,并从中选择一对相似三角形说明其为什么相似.
21、如图,PA切⊙O于点A,割线PBC交⊙O于B、C两点,∠APC的平分线分别交AC、AB于D、E两点.请在图中找出2对相似三角形,并从中选择一对相似三角形说明其为什么相似. 6、如图,PA切⊙O于点A,PBC是经过O点的割线,若∠P=30°,则弧AB的度数是( )
6、如图,PA切⊙O于点A,PBC是经过O点的割线,若∠P=30°,则弧AB的度数是( )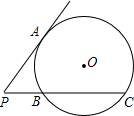 如图,PA切⊙O于点A,PBC是⊙O的割线,若PB=BC=2,则PA=
如图,PA切⊙O于点A,PBC是⊙O的割线,若PB=BC=2,则PA= 如图,PA切⊙O于点A,PBC是经过圆心的割线,并与圆相交于点B,C.若PC=9,PA=3,则∠P的余弦值是( )
如图,PA切⊙O于点A,PBC是经过圆心的割线,并与圆相交于点B,C.若PC=9,PA=3,则∠P的余弦值是( )