题目内容
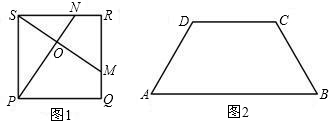
(1)填空:如图1,在正方形PQRS中,已知点M、N分别在边QR、RS上,且QM=RN,连接PN、SM相交于点O,则∠POM=(2)如图2,在等腰梯形ABCD中,已知AB∥CD,BC=CD,∠ABC=60度.以此为部分条件,
 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明.
分析:(1)根据正方形的性质容易得到全等条件证明△PSN≌△SRM,然后利用全等三角形的性质就可以得到∠POM=90°.
(2)根据已知条件构造命题要抓住它们的相同的地方,有三条邻边相等,并且已知一个角.命题的证明主要利用题目的已知条件证明△DCE≌△ADF,然后利用全等三角形的性质证明结论.
(2)根据已知条件构造命题要抓住它们的相同的地方,有三条邻边相等,并且已知一个角.命题的证明主要利用题目的已知条件证明△DCE≌△ADF,然后利用全等三角形的性质证明结论.
解答:解:(1)90,(2分)
∵QM=RN,
∴RM=SN,
∵∠PSN=∠SRM=90°,SP=SR,
∴△PSN≌△SRM,
∴∠SPN=∠RSM,
∵∠RSM+∠MSP=90°,
∴∠POM=90°
(2)构造的命题为:
已知等腰梯形ABCD中,AB∥CD,且BC=CD,∠ABC=60°,若点E、F分别在BC、CD上,且BE=CF,连接AF、DE相交于G,则∠AGE=120°.(4分)
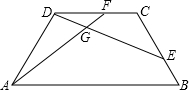
证明:由已知,在等腰梯形ABCD中,AB∥CD,且BC=DA,∠ABC=60°,
∴∠ADC=∠C=120°,
∵BC=CD,BE=CF,
∴CE=DF;(5分)
在△DCE和△ADF中,
∴△DCE≌△ADF(SAS),
∴∠CDE=∠DAF,(7分)
又∠DAF+∠AFD=180°-∠ADC=60°,
∴∠CDE+∠AFD=60°,
∴∠AGE=∠DGF=180°-(∠CDE+∠AFD)=180°-60°=120°.(8分)
∵QM=RN,
∴RM=SN,
∵∠PSN=∠SRM=90°,SP=SR,
∴△PSN≌△SRM,
∴∠SPN=∠RSM,
∵∠RSM+∠MSP=90°,
∴∠POM=90°
(2)构造的命题为:
已知等腰梯形ABCD中,AB∥CD,且BC=CD,∠ABC=60°,若点E、F分别在BC、CD上,且BE=CF,连接AF、DE相交于G,则∠AGE=120°.(4分)

证明:由已知,在等腰梯形ABCD中,AB∥CD,且BC=DA,∠ABC=60°,
∴∠ADC=∠C=120°,
∵BC=CD,BE=CF,
∴CE=DF;(5分)
在△DCE和△ADF中,
|
∴△DCE≌△ADF(SAS),
∴∠CDE=∠DAF,(7分)
又∠DAF+∠AFD=180°-∠ADC=60°,
∴∠CDE+∠AFD=60°,
∴∠AGE=∠DGF=180°-(∠CDE+∠AFD)=180°-60°=120°.(8分)
点评:此题是开放性试题,考查学生对正方形,梯形的性质及全等三角形的判定的综合运用.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 48、读句画图并填空:
48、读句画图并填空:
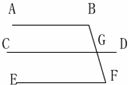 8、推理填空,如图,∵∠B=
8、推理填空,如图,∵∠B=
 阅读并填空:
阅读并填空: