题目内容
(1)解方程:| 2 |
| x |
| 2 |
| x(x+1) |
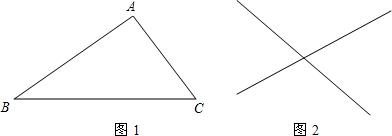
(2)已知△ABC(如图1),请用直尺(没有刻度)和圆规,作一个平行四边形,使它的三个顶点恰好是△ABC的三个顶点(只需作一个,不必写作法,但要保留作图痕迹)
(3)根据题意,完成下列填空:
如图2,L1与L2是同一平面内的两条相交直线,它们有1个交点,如果在这个平面内,再画第3直线L3,那么这3条直线最多可有
分析:(1)首先把分式两边乘以最简公分母x(x-1)去分母,然后去括号,移项,合并同类项,解出x的值,最后一定要检验.
(2)根据作已知∠B=∠CBD,再截取CD=AB即可;
(3)根据3条直线最多可有 3,个交点;4条直线最多可有 6个交点.由此我们可以猜想:在同一平面内,6条直线最多可有 15个交点,得出规律求出即可.
(2)根据作已知∠B=∠CBD,再截取CD=AB即可;
(3)根据3条直线最多可有 3,个交点;4条直线最多可有 6个交点.由此我们可以猜想:在同一平面内,6条直线最多可有 15个交点,得出规律求出即可.
解答:解:(1)去分母得:2(x+1)-2=x(x+1),
去括号得:2x+2-2=x2+x,
移项得:2x-x-x2=0
合并同类项得:-x2+x=0,
分解因式得:x(1-x)=0,
∴x=0或1,
检验:把x=1,代入最简公分母x(x-1)=0,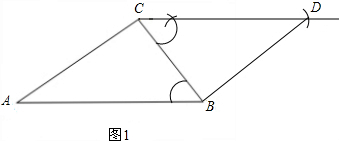
把x=0,代入最简公分母x(x-1)=0,
所以x=0或1都不是原方程的解.
∴原分式方程的解为:无解.
(2)如图所示;
(3)根据3条直线最多可有3个交点;4条直线最多可有6个交点.
由此我们可以猜想:在同一平面内,6条直线最多可有 15个交点,
∴n(n为大于1的整数)条直线最多可有( 1+2+…+n)个交点,
∴1+2+…+n=
,
故答案为:3,6,15,
.
去括号得:2x+2-2=x2+x,
移项得:2x-x-x2=0
合并同类项得:-x2+x=0,
分解因式得:x(1-x)=0,
∴x=0或1,
检验:把x=1,代入最简公分母x(x-1)=0,

把x=0,代入最简公分母x(x-1)=0,
所以x=0或1都不是原方程的解.
∴原分式方程的解为:无解.
(2)如图所示;
(3)根据3条直线最多可有3个交点;4条直线最多可有6个交点.
由此我们可以猜想:在同一平面内,6条直线最多可有 15个交点,
∴n(n为大于1的整数)条直线最多可有( 1+2+…+n)个交点,
∴1+2+…+n=
| n(1+n) |
| 2 |
故答案为:3,6,15,
| n(1+n) |
| 2 |
点评:此题主要考查了分式方程的解法,以及直线交点求法,做题过程中关键是不要忘记检验,很多同学忘记检验,导致错误.

练习册系列答案
相关题目