题目内容
 阅读并填空:
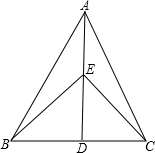
阅读并填空:如图:在△ABC中,AB=AC,AD⊥BC,垂足为点D,点E在AD上,点F在AD的延长线上,且CE∥BF,试说明DE=DF的理由.
解:因为AB=AC,AD⊥BC,
所以BD=
CD
CD
. (等腰三角形底边上的高与底边上的中线、顶角的平分线重合
等腰三角形底边上的高与底边上的中线、顶角的平分线重合
)因为CE∥BF,
所以
∠CEF
∠CEF
=∠BFE
∠BFE
,∠EDC=∠BDF(对顶角相等)在△BFD和△CED中,
所以△BFD≌△CED,(
AAS
AAS
)从而DE=DF.(
全等三角形对应边相等
全等三角形对应边相等
).分析:根据已知条件判定两三角形全等并利用全等三角形的对应边相等得到线段DE=DF的长即可;
解答:解:∵AB=AC,AD⊥BC,
∴BD=CD. ( 等腰三角形底边上的高与底边上的中线、顶角的平分线重合)
∵CE∥BF,
∴∠CEF=∠BFE,∠EDC=∠BDF(对顶角相等)
在△BFD和△CED中,
∴△BFD≌△CED(AAS)
∴DE=DF(全等三角形对应边相等).
故答案为:CD,等腰三角形底边上的高与底边上的中线、顶角的平分线重合,∠CEF=,∠BFE,AAS,全等三角形对应边相等.
∴BD=CD. ( 等腰三角形底边上的高与底边上的中线、顶角的平分线重合)
∵CE∥BF,
∴∠CEF=∠BFE,∠EDC=∠BDF(对顶角相等)
在△BFD和△CED中,
|
∴△BFD≌△CED(AAS)
∴DE=DF(全等三角形对应边相等).
故答案为:CD,等腰三角形底边上的高与底边上的中线、顶角的平分线重合,∠CEF=,∠BFE,AAS,全等三角形对应边相等.
点评:本题考查了全等三角形的判定与性质,通常利用全等三角形证明线段相等或角相等.

练习册系列答案
相关题目
 阅读并填空:
阅读并填空: 阅读并填空:
阅读并填空: 阅读并填空:
阅读并填空: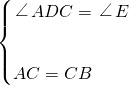
 阅读并填空:
阅读并填空: