题目内容
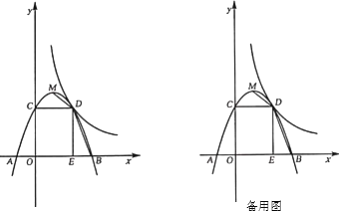
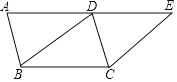
【题目】如图1,等腰梯形OABC的底边OC在x轴上,AB∥OC,O为坐标原点,OA = AB =BC,∠AOC=60°,连接OB,点P为线段OB上一个动点,点E为边OC中点.
(1)连接PA.PE,求证:PA=PE;
(2)连接PC,若PC+PE=2![]() ,试求AB的最大值;
,试求AB的最大值;
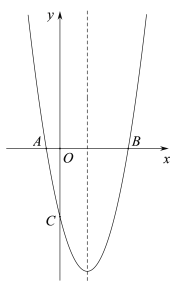
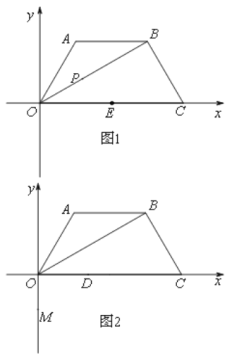
(3)在(2)在条件下,当AB取最大值时,如图2,点M坐标为(0,-1),点D为线段OC上一个动点,当D点从O点向C点移动时,直线MD与梯形另一边交点为N,设D点横坐标为m,当△MNC为钝角三角形时,求m的范围.
【答案】(1)详见解析;(2)AB的最大值为2;(3)当0<m< ![]() 或
或![]() <m<4时,△MNC为钝角三角形.
<m<4时,△MNC为钝角三角形.
【解析】
(1)连接AE,先证明∠ABO=∠BOC,再证明△OAE为等边三角形即可得证;
(2)由PC+PE=2![]() ,可知PC+PA=2
,可知PC+PA=2![]() .根据三角形三边关系OB=AC≤PC+PA,列不等式即可;
.根据三角形三边关系OB=AC≤PC+PA,列不等式即可;
(3)当AB取最大值时,AB=OA=BC=2,OC=4.分三种情况讨论:①当N点在OA上时,如图2,若CN⊥MN时,此时线段OA上N点下方的点(不包括N、O)均满足△MNC为钝角三角形。
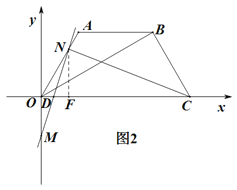
②当N点在AB上时,不能满足△MNC为钝角三角形;@当N点在BC上时,如图3,若CN⊥MN时,此时BC上N点下方的点(不包括N、C)均满足△MNC为钝角三角形.
解:(1)证明:如图1,连接AE.
∵OA=AB..∠A0B=∠ABO.
∴AB∥OC,∠ABO=∠BOC.
∴∠AOC=60°,∠A0B=∠BOC=30°,∠0BC=90°
∵E为OC的中点,∴OC=2BC=2OA;△OAE为等边三角形
∴OB垂直平分线段AE
∴PA=PE.

(2)∵PC+PE=![]() ,∴PC+PA=
,∴PC+PA=![]() .
.
显然有OB=AC≤PC+PA=![]()
在Rt△BOC中,设AB=OA=BC=x,则OC=2x,OB=![]() ,
,
∴![]() ≤
≤![]() ,∴
,∴![]() ≤2.
≤2.
即AB的最大值为2.
(3) 当AB取最大值时,AB=OA=BC=2,OC=4.
分三种情况讨论:
①当N点在OA上时,如图2,若CN⊥MN时,此时线段OA上N点下方的点(不包括N.O)均满足△MNC为钝角三角形.
过N作NF⊥x轴,垂足为F,
∵A点坐标为(1,![]() ),∴ 可设N点坐标为(a,
),∴ 可设N点坐标为(a,![]() a),
a),
则DF=a-m,NF=![]() a,FC=4-a.
a,FC=4-a.
∵△OMD∽△FND∽△FCN,
∴![]() .
.
解得,![]() ,即当0<m<
,即当0<m<![]() 时,△MNC为钝角三角形
时,△MNC为钝角三角形
②当N点在AB上时,不能满足△MNC为钝角三角形;

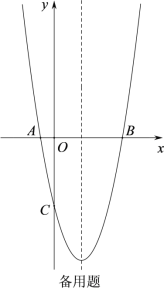
③当N点在BC上时,如图3,若CN⊥MN时,此时BC上N点下方的点(不包括N.C)均满足△MNC为钝角三角形.
∵OB⊥BC, CN⊥MN,. MN//OB.
∴∠ODM=∠BOC=30°
∴ OM=1,. OD=m=![]() .
.
∴当![]() <m<4时,△MNC为钝角三角形.
<m<4时,△MNC为钝角三角形.
综上所述,当0<m<![]() 或
或![]() <m<4时,△MNC为钝角三角形.
<m<4时,△MNC为钝角三角形.

【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 21 | 42% |
良好 | m | 40% |
合格 | 6 | n% |
待合格 | 3 | 6% |

请根据以上信息,解答下列问题:
(1)本次调查随机抽取了 名学生;表中m= ,n= ;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.