Question

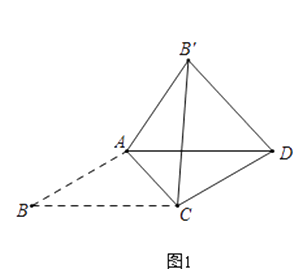
【题目】如图，将ABCD的边AB延长到点E，使BE=AB，连接DE，交边BC于点F．
（1）求证：△BEF≌△CDF；
（2）连接BD、CE，若∠BFD=2∠A，求证：四边形BECD是矩形．

Answer 1

【答案】
（1）证明：∵四边形ABCD是平行四边形，

∵AB=CD，AB∥CD．

∵BE=AB，

∴BE=CD．

∵AB∥CD，

∴∠BEF=∠CDF，∠EBF=∠DCF，

在△BEF与△CDF中，

∵ ，

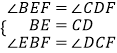∴△BEF≌△CDF（ASA）

（2）证明：∵四边形ABCD是平行四边形，

∴AB∥CD，AB=CD，∠A=∠DCB，

∵AB=BE，

∴CD=EB，

∴四边形BECD是平行四边形，

∴BF=CF，EF=DF，

∵∠BFD=2∠A，

∴∠BFD=2∠DCF，

∴∠DCF=∠FDC，

∴DF=CF，

∴DE=BC，

∴四边形BECD是矩形

【解析】（1）先根据平行四边形的性质得出AB=CD，AB∥CD，再由BE=AB得出BE=CD，根据平行线的性质得出∠BEF=∠CDF，∠EBF=∠DCF，进而可得出结论；（2）根据平行四边形的性质可得AB∥CD，AB=CD，∠A=∠DCB，再由AB=BE，可得CD=EB，进而可判定四边形BECD是平行四边形，然后再证明BC=DE即可得到四边形BECD是矩形
【考点精析】本题主要考查了平行四边形的性质和矩形的判定方法的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形才能正确解答此题．