题目内容
【题目】已知抛物线ykx24kx3kk0与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为D.
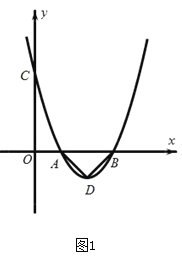
(1)如图1,请求出A、B两点的坐标;
(2)点E为x轴下方抛物线ykx24kx3kk0上一动点.
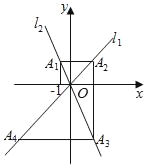
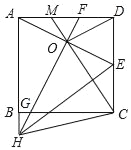
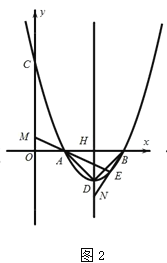
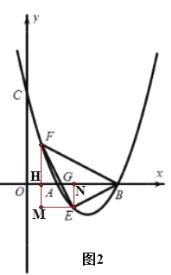
①如图2,若k=1时,抛物线的对称轴DH交x轴于点H,直线AE交y轴于点M,直线BE交对称轴DH于点N,求MONH的值;
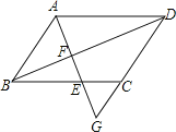
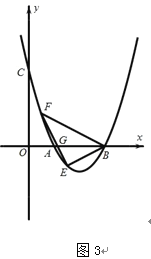
②如图3,若k2时,点F在x轴上方的抛物线上运动,连接EF交x轴于点G,且满足FBAEBA,当线段EF运动时,FGO的度数大小发生变化吗?若不变,请求出tanFGO的值;若变化,请说明理由.
【答案】(1)A(1,0)、B(3,0);(2)①![]() ,②不会变化,
,②不会变化,![]() 4.
4.
【解析】
(1)令ykx24kx3k=0,求得x1=1,x2=3,故A(1,0)B(3,0)
(2)①过点 E作 EK x轴于点k ,设 E(m, m24m3),易证BKE ∽ BHN , AKE ∽ AOM ,则![]() ,故
,故![]() ,
,![]() ,求出NH m 1, MO m 3得
,求出NH m 1, MO m 3得![]() ;②过点 E 作 EN x轴于点N,作FH x轴于点H过点 E
;②过点 E 作 EN x轴于点N,作FH x轴于点H过点 E
作 EM FH , 交 FH 的延长线于点 M,设 F (n,2n2 8n 6), E(a,2a2 8a 6)当n 3 时,不能满足FBA EBA ,当 n 1,由FHB ∽ ENB,则![]() ,
,
故![]() ,得:n a 2
,得:n a 2![]() ,
,
8 2(n a) 4为定值,即tan FGO 的值不变.
解:(1)令ykx24kx3k=0,求得x1=1,x2=3,故A(1,0)B(3,0)
(2)① y x24x3 ,如图 1 过点 E作 EK x轴于点k ,
∵KE∥HN∥x轴,∴BKE ∽ BHN, AKE ∽ AOM ,设 E(m, m24m3)
![]() ,即:
,即:![]() ,
,![]()
得: NH m 1, MO m 3
![]()
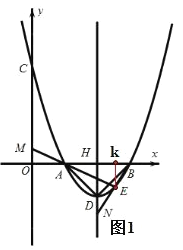
②不会变化。如图 2 过点 E 作 EN x轴于点N,作FH x轴于点H过点 E
作 EM FH , 交 FH 的延长线于点 M,
设 F (n,2n2 8n 6), E(a,2a2 8a 6)当n 3 时,
不能满足FBA EBA ,
当 n 1,FBAEBA,∴FHB ∽ ENB,则![]() ,
,
![]() ,
,
得: n a 2
![]() ,
,
8 2(n a) 4
综上可知:当点 F 和 E 在抛物线上运动时, tan FGO 的值不会发生变化, 且tan FGO 4

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案