题目内容
【题目】如图1,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.
(1)求证:四边形ABCD是平行四边形;
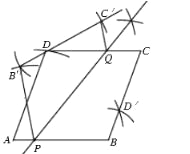
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由).

【答案】(1)详见解析;(2)图见解析.
【解析】试题解析:(1)根据已知条件易证AB∥CD,根据两组对边分别平行的四边形是平行四边形即可判定四边形ABCD是平行四边形;(2)根据轴对称的性质作图即可.
试题分析:
(1)四边形ABCD是平行四边形
证明:∵在四边形ABCD中,AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形;
(2)四边形PB′C′Q如下:

练习册系列答案
相关题目