题目内容
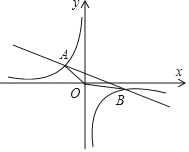
【题目】如图，反比例函数y=
（k≠0）的图象与一次函数y=﹣
x+1的图象交于A（﹣2，m），B（n，﹣1）两点．
（1）求反比例函数的解析式；
（2）连接OA，OB，求△AOB的面积．
【答案】(1)y=-
;(2)3.
【解析】分析：（1）把A（﹣2，m）代入y=﹣
x+1求出点A的坐标，再把点A的坐标代入y=
求出反比例函数解析式；
（2）把点B（n，﹣1）代入反比例函数y=﹣，求出点B的坐标，设一次函数y=﹣x+1的图象与x轴的交点为C，根据S△AOB=S△AOC+S△BOC求解即可.
详解：（1）因为点A（﹣2，m）在一次函数y=﹣x+1的图象上，
∴m=﹣×（﹣2）+1=2
即点A（﹣2，2）
∵点A（﹣2，2）在反比例函数y=
（k≠0）的图象上，
∴k=（﹣2）×2=﹣4．
所以反比例函数解析式为：y=﹣
；
（2）∵点B（n，﹣1）在反比例函数y=﹣
，
∴n×（﹣1）=4，
∴点B的坐标为（4，﹣1）
设一次函数y=﹣x+1的图象与x轴的交点为C，
当y=0时，﹣x+1=0，
解得x=2．
∴点C的坐标为（2，0）
所以S△AOB=S△AOC+S△BOC=×2×2+×2×1=3．
练习册系列答案
相关题目
