题目内容
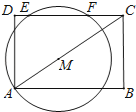
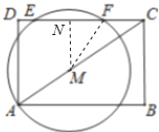
【题目】如图、矩形ABCD中,AB=8,AD=6.点M是对角线AC上的一个动点,以M点为圆心,线段AM长为半径画一个⊙M,若⊙M在以C为端点的矩形ABCD边上截得的线段EF=![]() AM,则线段AM的长是 .
AM,则线段AM的长是 .
【答案】![]() 或5.
或5.
【解析】
试题分析:作MN⊥EF于N,连接MF,由垂径定理得出EN=FN=![]() EF,设AM=5x,则MF=5x,EF=6x,得出FN=3x,由勾股定理得出MN=4x,由矩形的性质和勾股定理求出AC,由平行线的性质得出比例式求出MN=
EF,设AM=5x,则MF=5x,EF=6x,得出FN=3x,由勾股定理得出MN=4x,由矩形的性质和勾股定理求出AC,由平行线的性质得出比例式求出MN=![]() (10﹣5x),得出方程
(10﹣5x),得出方程![]() (10﹣5x)=4x,解方程求出x,得出AM;当M为AC的中点时,AM=MC,得出方程,解方程求出x,得出AM即可.
(10﹣5x)=4x,解方程求出x,得出AM;当M为AC的中点时,AM=MC,得出方程,解方程求出x,得出AM即可.
解:作MN⊥EF于N,连接MF,如图所示:
则EN=FN=![]() EF,∠MNF=90°,
EF,∠MNF=90°,
∵EF=![]() AM,
AM,
∴设AM=5x,则MF=5x,EF=6x,
∴FN=3x,
由勾股定理得:MN=![]() =4x,
=4x,
∵四边形ABCD是矩形,
∴BC=AD=6,∠D=∠B=90°=∠MNF,
∴AC=![]() =10,MN∥AD,
=10,MN∥AD,
∴![]() ,
,
即![]() ,
,
解得:MN=![]() (10﹣5x),
(10﹣5x),
∴![]() (10﹣5x)=4x,
(10﹣5x)=4x,
解得:x=![]() ,
,
∴AM=![]() ;
;
当M为AC的中点时,AM=MC,
即5x=10﹣5x,
解得:x=1,
∴AM=5;
综上所述:线段AM的长是![]() 或5.
或5.
故答案为:![]() 或5.
或5.

练习册系列答案
相关题目