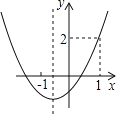Question

【题目】如图，点A（1，m2）、点B（2，m﹣1）是函数y＝（其中x＞0）图象上的两点．

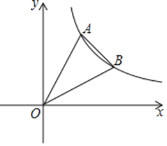
（1）求点A、点B的坐标及函数的解析式；

（2）连接OA、OB、AB，求△AOB的面积．

Answer 1

【答案】（1）A（1，2），B（2，1），函数的解析式为y＝；（2）

【解析】

（1）根据反比例函数图象上的点的坐标特征，得到k＝m2＝2（m﹣1），解得m的值，即可求得点A、点B的坐标及函数的解析式；

（2）由反比例函数系数k的几何意义，根据S△AOB＝S△AOM+S梯形AMNB﹣S△BON＝S梯形AMNB即可求解．

（1）点A（1，m2）、点B（2，m﹣1）是函数y＝（其中x＞0）图象上的两点，

∴k＝m2＝2（m﹣1），解得：m＝2，k＝2，

∴A（1，2），B（2，1），函数的解析式为：y＝；

（2）作AM⊥x轴于M，BN⊥x轴于N，

∴S△AOM=S△BON=k，

∴S△AOB＝S△AOM+S梯形AMNB﹣S△BON＝S梯形AMNB＝（2+1）（2﹣1）＝．