题目内容
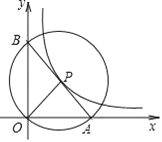
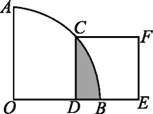
【题目】如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,阴影部分的面积为________
时,阴影部分的面积为________
【答案】2π-4
【解析】
连结OC,根据在同圆中,等弧所对的圆心角相等可得∠COD=45°,从而证出△ODC为等腰直角三角形,OD=CD=2![]() ,即可求出OC的长,然后根据阴影部分的面积=扇形BOC的面积-△ODC的面积,即可求出阴影部分的面积.
,即可求出OC的长,然后根据阴影部分的面积=扇形BOC的面积-△ODC的面积,即可求出阴影部分的面积.
解:连结OC,
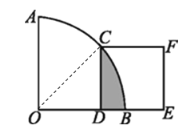
∵在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是 ![]() 的中点,
的中点,
∴∠COD=45°,
∴△ODC为等腰直角三角形,OD=CD=2![]()
∴OC= ![]() =4,
=4,
∵阴影部分的面积=扇形BOC的面积-△ODC的面积,
即S阴影= ![]() ×π×42-
×π×42- ![]() ×(2
×(2 ![]() )2=2π-4.
)2=2π-4.
故答案为:2π-4.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】每个人都应怀有对水的敬畏之心,从点滴做起,节水、爱水,保护我们生活的美好世界.某地近年来持续干旱,为倡导节约用水,该地采用了“阶梯水价”计费方法,具体方法:每户每月用水量不超过4吨的每吨2元;超过4吨而不超过6吨的,超出4吨的部分每吨4元;超过6吨的,超出6吨的部分每吨6元.该地一家庭记录了去年12个月的月用水量如下表,下列关于用水量的统计量不会发生改变的是( )
用水量x(吨) | 3 | 4 | 5 | 6 | 7 |
频数 | 1 | 2 | 5 | 4﹣x | x |
A. 平均数、中位数 B. 众数、中位数 C. 平均数、方差 D. 众数、方差