题目内容
【题目】如图，已知直线y1=x+m与x轴、y轴分别交于点A、B，与双曲线
（x<0）分别交于点C（-1，2）、D（a，1）．
（1）分别求出直线及双曲线的解析式；
（2）利用图象直接写出，当x在什么范围内取值时，y1>y2．
(3）请把直线
上y1<y2时的部分用黑色笔描粗一些.
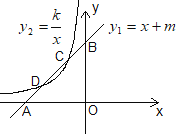
【答案】（1）一次函数的解析式：y=x+3,双曲线： 
；（2）
；（3）见解析.
【解析】试题分析：
（1）把点C（-1，2）分别代入： 
和
中解出
的值即可求得两个函数的解析式；
（2）把点D（a，1）代入（1）中所得的反比例函数的解析式（或一次函数的解析式）即可求得a的值，从而可得点D的坐标，这样结合点A的坐标即可求出
时，自变量
的取值范围；
（3）结合（2）中结论，按题中要求将图象中相应部分描粗一些即可.
试题解析：
（1）把点C（-1，2）坐标代入
，得m=3，
∴一次函数的解析式为： 
，
把点C（-1，2）坐标代入
，得k= -2，
∴反比例函数的解析式为： 
；
（2）把点D（a，1）坐标代入
，
∴ a=-2，
∴点D的坐标为（-2，1），
∴由图象可知，当
时， 
；
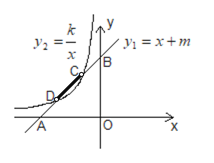
（3）由（2）可知：直线
的图象上，当y1<y2时所对应的部分是线段CD（不包括C、D两点的部分），按要求将这部分描粗如下图所示：
练习册系列答案
相关题目
