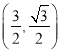题目内容
【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
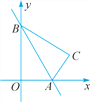
(2)从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于0.25,则n的值是 ;
(3)当n=2时,先从袋中任意摸出1个球不放回,再从袋中任意摸出1个球,请用列表或画树状图的方法,求两次都摸到白球的概率.
【答案】(1)摸到红球和摸到白球的可能性相同;
(2)2;
(3)
两次摸出的球颜色不同的概率=![]() =
=![]() .
.
【解析】
试题分析:(1)当n=1时,利用概率公式可得到摸到红球和摸到白球的概率都为![]() ;
;
(2)利用频率估计概率,则摸到绿球的概率为0.25,根据概率公式得到![]() =0.25,然后解方程即可;
=0.25,然后解方程即可;
(3)先画树状图展示所有12种等可能的结果数,再找出两次摸出的球颜色不同的结果数,然后根据概率公式求解.
试题解析:(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性相同;
(2)利用频率估计概率得到摸到绿球的概率为0.25,
则![]() =0.25,解得n=2,
=0.25,解得n=2,
故答案为2;
(3)解:画树状图为:

共有12种等可能的结果数,其中两次摸出的球都是的结白色的结果共有2 种,
所以两次摸出的球颜色不同的概率=![]() =
=![]() .
.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
【题目】某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是( )
纸笔测试 | 实践能力 | 成长记录 | |
甲 | 90 | 83 | 95 |
乙 | 88 | 90 | 95 |
丙 | 90 | 88 | 90 |
A. 甲 B. 乙、丙 C. 甲、乙 D. 甲、丙