题目内容
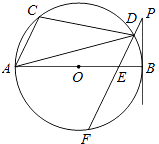
【题目】如图,直线 CB 和射线 OA,CB//OA,点 B 在点 C 的右侧.且满足∠OCB=∠OAB=100°,连接线段 OB,点 E、F 在直线 CB 上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠BOE
(2)当点 E、F 在线段 CB 上时(如图 1),∠OEC 与∠OBA 的和是否是定值?若是,求出这个值;若不是,说明理由。
(3)如果平行移动 AB,点 E、F 在直线 CB 上的位置也随之发生变化.当点 E、F 在点 C 左侧时,∠OEC 和∠OBA 之间的数量关系是否发生变化?若不变,说明理由;若变化,求出他们之间的关系式.

【答案】(1)![]() ;(2)
;(2)![]() ;(2)变化,
;(2)变化,![]() .
.
【解析】
(1)根据两直线平行,同旁内角互补求出![]() ,然后根据已知可得
,然后根据已知可得![]() ,由此计算即可得解;
,由此计算即可得解;
(2)根据两直线平行,同旁内角互补求出![]() ,再根据三角形的一个外角等于与它不相邻的两个内角的和可得
,再根据三角形的一个外角等于与它不相邻的两个内角的和可得![]() ,从而可得
,从而可得![]() ,由此即可解题;
,由此即可解题;
(3)同理(1)可得![]() ,根据三角形的内角和定理可知
,根据三角形的内角和定理可知![]() ,从而得到
,从而得到![]() ,由此计算即可得解.
,由此计算即可得解.
解:(1)![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
由(1)可知![]() ;
;
∴![]()
(3)变化,![]() ,
,
证明:当点 E、F 在点 C 左侧时,如图,

![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ;
;
∴![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
即:![]()

 阅读快车系列答案
阅读快车系列答案【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶 | 小瓶 | |
进价(元/瓶) | 5 | 2 |
售价(元/瓶) | 7 | 3 |
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?